Золотое сечение в строительстве: Золотое сечение при строительстве дома. Золотые пропорции вашего дома

Золотые пропорции вашего дома / Экодом своими руками

Золотые пропорции вашего дома

Сотворение поистине гармоничного пространства невозможно без ясного осознания принципов создания и обустройства своего жилища. Наши предки на протяжении тысяч лет накапливали опыт в строительстве как отдельных домов, так и целых поселений. В этой статье хочу рассказать вам о «золотой пропорции». О том, что даже в ученых кругах принято называть «фирменным знаком Бога» — пропорции по которой создано все живое и неживое во Вселенной: от завитушек раковины моллюска до спиралевидных завихрений галактик, а также и сам человек.

Человек – образец «золотой пропорции»

Человек – мера всех вещей. Это очень хорошо понимали наши предки.

Вот почему в основу исконной славянской измерительной системы были положены размеры частей тела человека, о чем говорят даже сами названия – сажень косая, маховая, локоть, стопа, пядь, пясть и т.д. Соответственно, меры длины уже заключали в себе «золотые пропорции», как и само тело человека воплощает в себе множество соотношений разных его частей.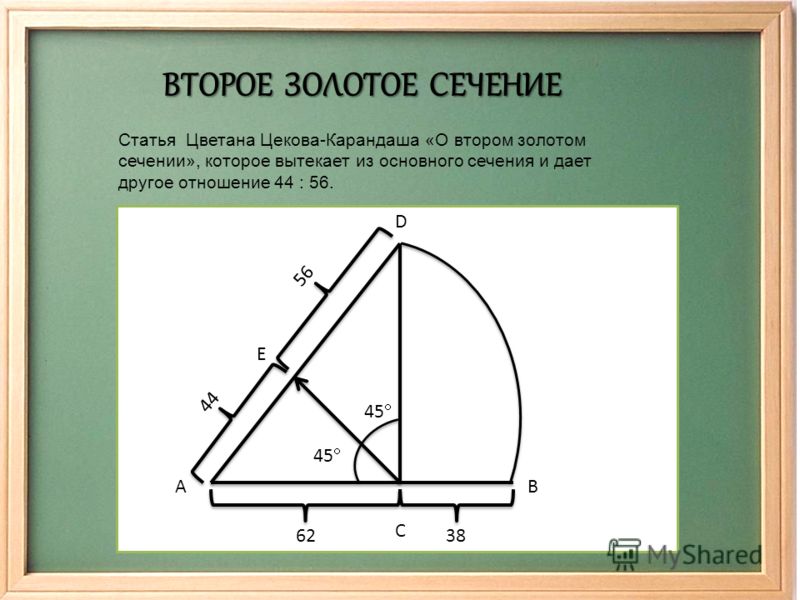 Вот поэтому строения, возведенные согласно древнерусским мерам длины и являли собой образцы гармонии и согласованности с окружающей природой!

]

Конечно же, в повседневном строительстве славянские мастера вряд ли прибегали к специальной точной подгонке своих расчетов к золотому числу 0,618, а соблюдение пропорций возникало благодаря развитой интуиции и использованию на Руси уникальной системы единиц измерения.

Свойства древнерусских «сажень»

Итак, в древнерусской числовой системе архитектурного планирования в качестве единиц измерения использовался набор инструментов под общим названием «сажени». Знаменательной особенностью древнерусской измерительной системы является то, что саженей на Руси существовало десятки, а то и сотни видов. Причем, в каждой местности могли быть свои сажени – черниговские, московские, владимирские, новгородские…(это могло быть связано с разным ростом людей из разных регионах и различиями в пропорциях их тел, ведь, например, северный человек отличается от южного). Да и любой знающий мастер мог изобрести не одну персональную сажень. И это не удивительно, ведь дом должен строиться под хозяина. Нам же не приходит в голову носить в качестве одежды прямоугольные коробки. Одежду мы подбираем, как говорится, «чтобы костюмчик сидел» — под свой рост, размер и пропорции тела. Так же и с домом. Невысокому человеку неуютно в доме для великана. Так же как и богатырю биться о низкие потолочные балки в доме с двухметровыми потолками ни к чему. Как говорится, все гениальное – просто.

Однако и это еще не все. Как показывают исследования древнерусские сажени, помимо прочего, сложно назвать соразмерными друг другу. Именно поэтому, современные исследователи полагают, что метрическая система, построенная на использовании эталонного метра, является более совершенной и удобной для использования в расчетах, чем система, построенная на многообразии саженей несоразмерных друг другу.

Возникает закономерный вопрос, чем же обусловлена вековая практика применения нашими Предками иррациональных инструментов соизмерения? Наука вряд ли даст нам ответ, а в утверждениях ученых видится однобокое, ограниченное материальное восприятие действительности и, часто, неумение проникнуть в суть явлений, постигнуть их глубинный смысл и предназначение.

Окружающая нас природа живет, пульсирует, дышит. Пульсируют как мельчайшие клетки, организмы, растения, животные, так и камни, планеты, звезды, в общем, все живое и неживое на Земле и в Космосе. Все движется, распространяя колебания в виде самых разнообразных волн. Точно также части зданий: стены, потолки, создают определенные вибрации уже в самом помещении. Эти вибрации почти не улавливаются приборами (точнее приборы, их улавливающие, еще не созданы, поскольку само явление не допускается), но очень хорошо ощущаются человеческим организмом. Отмечается, что во всех помещениях, построенных на основе метрической системы, существуют стоячие волны, отрицательно воздействующие на организм проживающих в них людей [Черняев А.Ф., «Золото Древней Руси»].

Более того, эти волны воздействуют на организм человека, подавляя его и вынуждая тратить свою энергию на сопротивление волновому воздействию, ослабляют его и способствуют заболеваниям. И чем больше стоячих волн в жилом помещении, тем больше энергии необходимо тратить организму на ее гашение.

Секрет создания гармоничного Родового Дома

Древнерусские сажени не являются в численном выражении рациональными инструментами, и потому не имеют кратного ни себе, ни своим частям делителя. Отсутствие кратности расстояния приводит к разбалансировке стоячих волн, а соразмерность пропорций человеческому телу – к возникновению волн, резонирующих с вибрациями человеческого организма, находящегося в нем. Такое помещение становится наилучшим для проживания людей. Именно такие, не имеющие кратности ни одному измерителю, ни в длину, ни в ширину, ни в высоту дома строили наши Предки. И, видимо, именно по этой причине в старинных домах и храмах люди чувствуют себя уютно, спокойно, благодатно и расслабленно, хотя и не понимают, что стоит за этим.

Надо признать, что метр хоть и является гениальным изобретением, но он годится только для измерения уже найденных пропорций, а планировать и строить на его основе нежелательно.

При строительстве же своего Родового Дома необходимо учитывать опыт и знаний наших Предков. Улучшение уже существующих жилищ можно производить путем визуальной разбивки помещения на части, соответствующие золотой пропорции.

Применение этих принципов на практике поможет оживить любое помещение, уменьшить образование неблагоприятных сил, а также будет способствовать более приятному и ладному виду вашего дома.

Родогор и Светояра Качуренко
vk.com/slavyanskie_uzori»>

Правило золотого треугольника в строительстве

Тайны ряда Фибоначчи: как работает принцип золотого сечения в архитектуре

Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.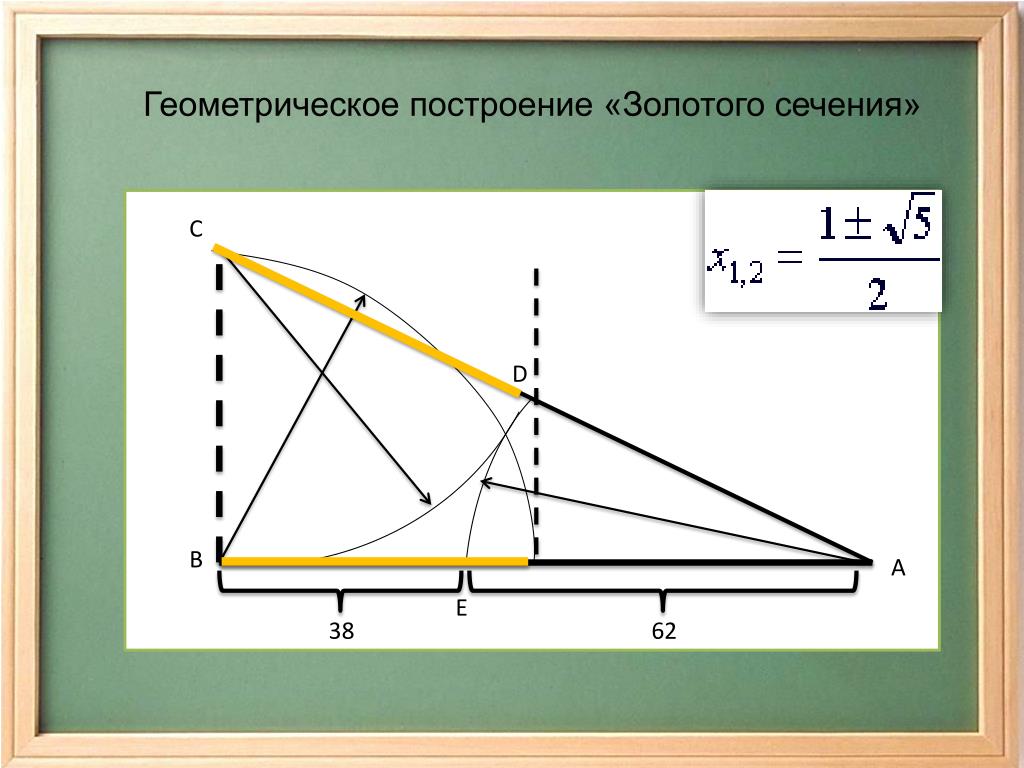 ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.

Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

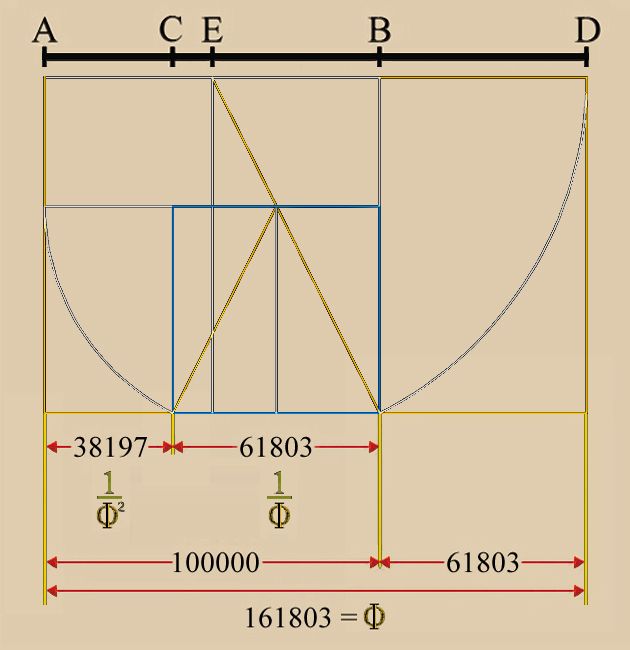
Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии.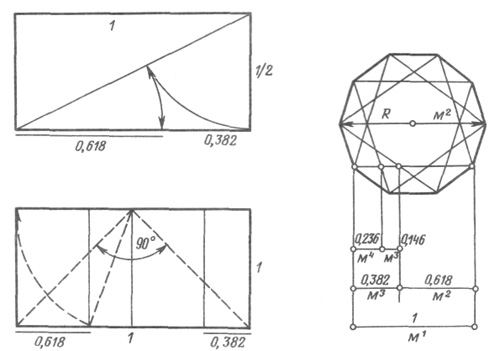 Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

• практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
• данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
• именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Экскурс в историю: кто придумал золотое сечение

Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:

• маленький отрезок – это сын;
• большой – отец;
• весь отрезок – это святой дух.

Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.

Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.

Золотое сечение в божественной пропорции

Принцип расчета и построения золотого сечения

Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.

Как определить число золотого сечения

С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:

• 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
• если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.

Ряд Фибоначчи в церкви Покрова на Нерли

Как рассчитать золотое сечение на простейшем примере

Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.

Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.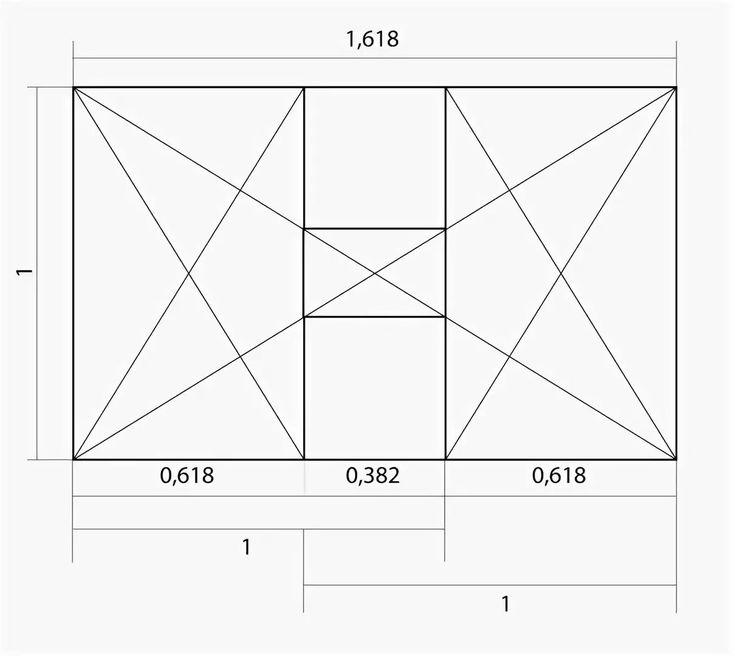

Простой пример золотого сечения в курином яйце

Как построить золотое сечение на примере прямоугольника и спирали

Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:

• нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
• над ними разместить квадрат со стороной 2;
• слева гармонично помещается квадрат с гранью 3;
• ниже – квадрат со стороной 5;
• справа пространство займет квадрат с гранью 8;
• площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
• если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
• если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

Построение золотой спирали из прямоугольника

На видео можно более подробно узнать про магию чисел Фибоначчи:

Как разметить фундамент своими руками

Содержание:

Прежде чем приступать к укладке фундамента, было бы неплохо грамотно сделать разметку. На первый взгляд – ничего сложного, но это пока не преступишь к делу. Как разметить фундамент своими руками? Первый совет: если вы еще не определились с материалами, из которых будете строить дом – определитесь. Нередко размер этих материалов может диктовать и размер фундамента.

С чего начать?

Чаще всего фундамент прямоугольной формы. Т.е на земле нам нужно разметить прямоугольник.

Начинаем разметку с обозначения первой стены. Нужно натянуть веревку между двумя колышками. Далее начинается самое интересное. От колышков (углов) нам нужно провести два перпендикуляра. Есть несколько способов, как это сделать: во-первых, заранее можно заготовить треугольник из ровных реек. Прикладываем треугольник к первому углу, и получаем направление, в котором пойдет перпендикулярная стена.

Второй способ для любителей поморочить себе голову. Но он отлично подойдет, если заранее вы не подготовились. Способ «египетского» или «золотого» треугольника. У такого треугольники стороны равны 3, 4 и 5 (удобнее брать эти единицы в метрах).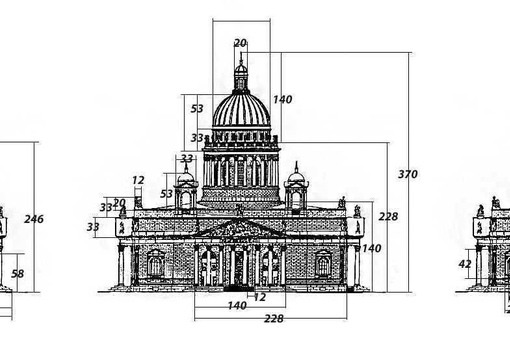 Нам понадобится веревка. На первом отрезке отмеряем 3м, вешаем в этом месте прищепку. От места пересечения шнурков отмеряем 4м, и тоже вешаем прищепку. Измеряем расстояние между 2-мя прищепками (с помощью рулетки). Оно должно быть равно 5м.

Когда вы отметите 4 угла будущего дома, приступайте к следующему этапу. Обноска. Она нужна для того, чтобы при выкапывании котлована под фундамент, ваша разметка не исчезла. Нужно вбить колья длиной 1,5м, чтобы 50см выступали над землей. На колышки набиваем планки размером 10см, чтобы натянутая веревка не сломала наши колышки.

Местонахождение шнура или веревки нужно обозначить яркой краской. Обноска сохраняется, пока фундамент не начнет «расти».

Общие правила разметки для любого фундамента

Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.

Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.

Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.

Правило золотого треугольника

Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.

Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.

Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21

Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.

Правила золотого треугольника (т.Пифагора)

Рассмотрим на примере построение прямоугольного фундамента с размерами 6х8м с помощью золотого треугольника (т. Пифагора).

1. Размечаем первую сторону фундамента. Это самая простая часть в построении нашего прямоугольника. Главное, что нужно помнить. Если хотим чтобы наш фундамент (дом) был параллелен одной из сторон забора либо другого объекта на участке или за его пределами, то первую линию нашего фундамента делаем равноудаленной от выбранного нами объекта. Данную процедуру мы описывали выше. Для размещения первой бечевки можно использовать колушки, прочно закрепленные в грунте, но в идеальном варианте для данной цели использовать обноску. Ее и будем использовать. Расстояние между обносками для данной стороны сделаем 14м: между обносками и будущими углами по 3м и 8м под фундамент.

2. Натягиваем вторую бечевку максимально перпендикулярно первой. Идеально перпендикулярно на практике натянуть сложно, поэтому на рисунке мы также отобразили ее не много отклоненной.

3. Скрепляем обе бечевки в точке пересечения. Скрепить можно скобкой либо скотчем. Главное чтобы надежно.

4. Приступаем к формированию прямого угла с применением теоремы Пифагора. Будем строить прямоугольный треугольник с катетами 3 на 4 метра и гипотенузой 5 метров. Для начала отмеряем на первой бечевке 4 метра от места пересечения бечевок, а на второй 3 метра. Ставим отметки на шнурке с помощью скотча (прищепка и т.п.).

5. Соединяем рулеткой обе отметки. Один конец рулетки фиксируем у отметки в 4 метра и ведем в сторону отметки в 3 метра на другой бечевке.

6. Если у нас прямоугольный треугольник, то обе отметки должны сойтись при расстоянии в 5 метров. В нашем случае отметки не сошлись. Поэтому перемещаем бечевку в нашем случае вправо до того момента когда отметка на 3 м совпадет с делением рулетки на 5 м.

7. В итоге у нас получился прямоугольный треугольник с углом в 90⁰ между двумя бечевками.

8. Больше отметки нам не нужны и их можно убрать.

Заканчиваем разметку фундамента и проверяем размеры

Завершающей стадией разметки является замер отступа от лицевой стороны стены для фундамента. Лицевую сторону будущего котлована отмечают на поверхности ровной доской, и фиксируют ее колышками. Точно такую же процедуру нужно выполнить с обозначением наружных стен по всему периметру.

Разметка фундамента – дело довольно-таки ответственное. Одно неровное движение, и ваше будущее строение под угрозой. Как говорится, семь раз отмерь… В данном случае эта пословица очень актуальна. Будет обидно, если у фас получится не прямоугольный фундамент, а фигура, не имеющая классификации.

Рассчитываем, что данная статья помогла ответить вам на вопрос: «Как разметить фундамент своими руками?».

Видео разметки фундамента своими руками

Разметка под фундамент своими руками

Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент. Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.

Какие инструменты понадобятся?

Производится разметка фундамента своими руками с применением инструментов:

• Рулетки;
• Шнура;
• Гидроуровня и отвеса;
• Помимо этого понадобятся деревянные колышки.

С чего начать разметку?

Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.

«Египетский треугольник». Самый простой метод

Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:

1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего;
2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов;
3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками;
4. Вдоль короткой стороны проводят требуемый перпендикуляр;
5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.

Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения.

Paste a VALID AdSense code in Ads Elite Plugin options before activating it.

Метод двух дуг

Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.

На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.

Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).

Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.

разметка фундамента

Содержание:

Фундамент – это ключевая конструкция в любом строении. От качества проектирования фундаментов зданий и его сооружения напрямую зависит судьба дома. Любая даже самая мелкая ошибка можетпривести к непоправимым последствиям. Многие застройщики возводят основание дома своими силами. На самом деле это самая сложная работа, но к ее выполнению необходимо подходить ответственно. Сама работа по строительству фундамента начинается с его разметки и должна выполняться в строгом соответствии с рабочей документации.

Подготовка к разметке фундамента

Перед началом работы необходимо очистить будущую строительную площадку от мусора, удалить траву, устранить неровности, может быть придется засыпать низкие участки земельного участка. Другими словами убрать с территории все, что может помешать строительным работам. Кстати, высокая трава, может создать определенные погрешности при проведении разметки.

Разметка фундамента никак не влияет на прочностные параметры основания под дом. Но от качества ее выполнения зависят углы, длина стен, а иногда даже внутридомовая планировка. Разметка фундаментасвоими руками позволяет не только сэкономить определенную сумму, но при необходимости внести какие-либо коррективы.

В качестве примера разметки рассмотрим самый вариант, когда дом и земельный участок имеют прямоугольную форму. Последовательность действий будет выглядеть следующим образом.

Первым делом необходимо установить место, где будет размещаться дом. Необходимо выбрать самыеблизкие границы участка. Отступив от границ участка на определенное расстояние можно натянутьшнуры. Они покажут первый угол дома. Шнуры натягивают на заранее подготовленные колышки. Спомощью строительной рулетки, можно обозначить стены дома. После выполнения всех замеров можно между отмеченными точками натянуть шнуры. Это и будет контур будущего дома. На последнем этапе необходимо проверить размеченные углы.

Проверка диагоналей и исправление ошибок разметки фундамента

Если разметка под фундамент своими руками выполнена правильно, то диагонали прямоугольника, обозначающего контуры будущей постройки, будут равны. Погрешность должна быть минимальной. Практика показывает, что она должна лежать в пределах менее одного сантиметра. Если диагонали имеют разные размеры, то придется передвигать стороны полученного прямоугольника, до того, по диагонали не станут равны друг другу.

Разметка фундамента под дом инструменты

Перед тем, как сделать разметку под фундамент, надо приготовить строительную рулетку, колышки, к которым будет привязываться разметочный шнур. Для изготовления колышков целесообразно использовать прутья, нарезанные из строительной арматуры.

Кстати, для более точного выполнения разметки можно использовать геодезические инструменты. Может быть, даже имеет смысл пригласить специалистов по выполнению геодезических работ.

Правило золотого треугольника

Разметку фундамента под дом – можно выполнить с использованием «египетского треугольника». Он обладает сторонами, у которых длины составляют 3, 4, 5. Это могут быть метры, сантиметры. Для сборки этого инструмента потребуются рейки из дерева или металла. После сборки будет получен прямоугольный треугольник. Этот инструмент применяют для определения прямых углов и направления стен. Но, такой треугольник будет обладать довольно большими размерами, это определяет сложности при его сборке и им работать будет не очень удобно.

Правила расположения строений на участке

После приобретения земельного участка, некоторые домовладельцы сразу начинают его застройку. Но существуют нормативные документы, которые определяют правила застройки. И только руководствуясь этим требованиями можно расположить постройки по территории застройки. Если участок предназначен для индивидуального застройки, то при распределении вспомогательных сооружений на земельном участке надо ориентироваться на требования СП 30–102–99. Если на участке будет построена дача, то надо изучить СНиП 30–02–97.

Расстояния между постройками на участке относительно соседского участка

В строительном деле используется понятие – «красная линия». Это черта, которая разделяет строенияот дорог, проездов и пр.

Правила строительства здания на участке ИЖС допускают расположение дома на удалении не менее 5метров от красной линии улицы и не менее 3 метров от проездов. Хозяйственные постройки должны располагаться на удалении от улицы, как минимум 5 метров.

Кроме расстояния до красной линии, в этих документах определены расстояния от построек, возводимых на земельном участке, до соседнего дома. Например, удаление от дома до забора, должно составлять 3 метра, а построек другого назначения от 1 до 4 метров. Все расстояния должны измеряются от окон одного здания до стены другого.

Как разместить строения, на земельном участке, не нарушая противопожарные правила

Перед планировкой земельного участка, надо изучить правила пожарной безопасности. В них тоже обозначены расстояния между домами и постройками. Так, между домами, которые расположены на соседних участках минимальное расстояние должно составлять 6 метров. Этими правила и определены допустимые расстояние между постройками, размещаемых на земельном участке.

Расстояния между постройками на земельном участке

Для правильного размещения построек на собственном земельном участке застройщик должен строго соблюдать все правила, относящиеся к застройке. Для минимизации ошибок имеет смысл выполнить зонирование участка. То есть разделить его на зоны, в которых будут возводиться постройки разного назначения.

На земельном участке выделяют следующие зоны:

• жилая, в ней будет сооружаться дом;
• хозяйственная зона, в ней будет размещаться вспомогательные постройки;
• территорию отдыха, в ней можно построить площадку для игр, беседку;
• зона для размещения садовых деревьев, кустов и огорода.

Существующие нормы определили следующие требования к удалению между между жилым домом и вспомогательными строениями:

• от строений, площадью до 50 м2 – 15 м;
• от места расположения уборных, компостных ям, ям для сбора мусора – 15 м;
• от колодца, производительностью до 1 м3/сутки – 8 м, производительностью 3 м3/сутки — 10 м;
• от септика с пропускной способностью до 1 м3/сутки – 5 м, если количество отходов составляет от 1 до3 м3/сутки – 8 м.

Условия точного переноса плана на местность

Для того, чтобы чертеж фундамента было просто перенести на местность и произвести разметка под фундамент с необходимой точностью, необходимо выполнить некоторые условия.

Во-первых, необходимо соблюдения масштаба будущего строения. Для этого применяют масштабы 1:100, 1:200, 1:300, 1:400.

Во-вторых, перенос чертеж фундамента на местность существенно облегчит осевая разметка. Оси, наносят на план и в местах монтажа отдельных элементов строительной конструкции (колонны и пр.). Между осям обязательно должно быть указано расстояние. План фундамента и его чертеж – это основные рабочие документы при строительстве фундаментного основания.

Основные параметры расчетов

При создании чертежа основания дома, необходимо использовать результаты расчетов, совершенных при проектировании фундаментов. В частности, необходимо учесть:

• полную массу строящегося дома;
• рост нагрузки на дом в процессе его эксплуатации, например, возведение второго этажа;
• уровень подземных вод;
• вид грунта на земельном участке.

Эти данные учитывают не только геометрические размеры фундамента, но материалы, которые будут использованы при его сооружении (марка бетона, размер арматуры и пр.). Кроме этого, проектировщик определит тип гидравлической и тепловой изоляции. При строительстве фундамента не земле с высоким расположением грунтовых вод, необходимо спроектировать дренажную систему, которая будет отводить излишки воды от фундаментной конструкции, и тем самым продляя срок его эксплуатации.

В идеальном варианте, проектирование фундаментов зданий и сооружений должны, выполняться в компании, которая имеет опыт такой работы по проектированию оснований. При самостоятельном проектировании фундаментов зданий желательно использовать действующие руководства и инструкции по проектированию фундаментов.

Видео по теме разметка фундамента

1 разметка фундамента

2 разметка фундамента своими руками

Золотое сечение пропорция в строительстве дома

Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…

Что такое золотое сечение и как его понимать

Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.

О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.

Сохранившиеся постройки древности тоже подчинены правилу золотого сечения

Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.

Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

Принцип и формула золотого сечения

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.

Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.

Последовательность Фибоначчи — не только математическая формула

Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.

Как построить прямоугольник с идеальными пропорциями

Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Построение прямоугольника с золотым сечением

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Это явно неспроста. Хотя далеко не все подчиняется этой закономерности

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.

Как разделить отрезок по правилу золотого сечения

Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Ничего особенного, но взгляд не оторвать. Знаете почему?

Итак, порядок деления отрезка по правилу золотого сечения:

• Берем отрезок, делим его пополам.
• Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
• Полученную точку C соединяем прямой с другим концом отрезка (A).
• На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
• Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
• Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Деление отрезка на участки с идеальным соотношением

Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

• Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
• Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

• Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
• Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

Применение в строительстве

Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Исаакиевский собор — можете посчитать ради интереса

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.

Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.

Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.

Золотое соотношение во внутреннем оформлении

Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:

• Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
• Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
• При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
• При выборе цвета придерживайтесь примерно тех же правил:

• Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.

• Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.

Пример подбора цвета по правилам правильной пропорциональности

Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Пропорциональность — важная вещь

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.

Золотое сечение в ландшафтном дизайне

При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

Правило треугольника в садовом дизайне

От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.

Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.

Каждый человек, сталкивающийся с геометрией объектов в пространстве, хорошо знаком с методом золотого сечения. Его применяют в искусстве, дизайне интерьеров и архитектуре. Еще в прошлом столетии золотое сечение оказалось таким популярным, что теперь многие сторонники мистического видения мира дали ему другое название – универсальное гармоническое правило. Особенности этого метода стоит рассмотреть подробнее. Это поможет узнать, почему он пользуется интересом сразу в нескольких сферах деятельности – искусстве, архитектуре, дизайне.

Суть универсальной пропорции

Принцип золотого сечения является всего лишь зависимостью чисел. Однако многие относятся к нему предвзято, приписывая этому явлению какие-то мистические силы. Причина кроется в необычных свойствах правила:

• Многие живые объекты обладают пропорциями туловища и конечностей, приближенными к показаниям золотого сечения.
• Зависимости 1,62 или 0,63 определяют отношения размеров лишь для живых существ. Объекты, относящиеся к неживой природе, очень редко соответствуют значению гармонического правила.
• Золотые пропорции строения туловища живых существ представляют собой неотъемлемое условие выживания многих биологических видов.

Золотое сечение можно найти в строении тел различных животных, стволов деревьев и корней кустарников. Сторонники универсальности этого принципа стараются доказать, что его значения жизненно важны для представителей живого мира.

Можно объяснить метод золотого сечения, используя образ куриного яйца. Отношение отрезков от точек скорлупы, в равной степени удаленных от центра тяжести, равно показателю золотого сечения. Самым важным для выживания птиц показателем яйца является именно его форма, а не прочность скорлупы.

Происхождение золотого сечения

Об универсальном правиле было известно еще математикам Древней Греции. Ее использовал Пифагор и Евклид. В известном архитектурном шедевре – пирамиде Хеопса отношение размеров основной части и длины сторон, а также барельефов и декоративных деталей соответствуют гармоническому правилу.

Метод золотого сечения взяли на вооружение не только архитекторы, но и художники. Тайна гармонической пропорции считалась одной из величайших загадок.

Первым, документально заверившим универсальную геометрическую пропорцию, был монах-францисканец Лука Пачоли. Его способности к математике были блестящи. Широкое признание золотое сечение получило после публикации результатов исследований золотого сечения Цейзинга. Он изучал пропорции тела человека, древние памятники скульптуры, растения.

Как рассчитали золотое сечение

Разобраться, что такое золотое сечение, поможет объяснение, основанное на длинах отрезков. К примеру, внутри большого находится несколько маленьких. Тогда длины небольших отрезков относятся к общей длине большого отрезка, как 0,62. Такое определение помогает разобраться, на сколько частей можно поделить определенную линию, чтобы она соответствовала гармоническому правилу. Еще один плюс использования этого метода – можно узнать, каким должно быть отношение самого большого отрезка к длине всего объекта. Это соотношение равняется 1,62.

Такие данные можно представить, как пропорции измеряемых объектов. Сначала их выискивали, подбирая опытным путем. Однако теперь точные соотношения известны, поэтому построить объект в соответствии с ними не составит труда. Золотое сечение находят такими путями:

• Построить прямоугольный треугольник. Разбить одну из его сторон, а затем провести перпендикуляры с секущими дугами. При проведении вычислений следует от одного конца отрезка построить перпендикуляр, равный ½ его длины. Затем достраивают прямоугольный треугольник. Если отметить точку на гипотенузе, которая покажет длину перпендикулярного отрезка, то радиус, равняющийся оставшейся части линии, рассечет основание на две половины. Получившиеся линии будут соотноситься друг с другом согласно золотому сечению.
• Универсальные геометрические значения получают и другим способом – выстраивая пентаграмму Дюрера. Она является звездой, которая помещена в окружность. В ней находится 4 отрезка, длины которых соответствуют правилу золотого сечения.
• В архитектуре гармоническая пропорция применяется в модифицированном виде. Для этого прямоугольный треугольник следует разбивать по гипотенузе.

Если в традиционном толковании гармонического правила для графики, его рассчитывали как 37:63, то для архитектурных сооружений чаще использовали 44:56. Это обусловлено необходимостью сооружать высотные постройки.

Секрет золотого сечения

Если в случае с живыми объектами золотое сечение, проявляющееся в пропорциях тела людей и животных можно объяснить необходимостью приспосабливаться к среде, то в использование правила оптимальных пропорций в 12 веке для постройки домов было в новинку.

Парфенон, сохранившийся со времен Древней Греции, был возведен по методу золотого сечения. Множество замков вельмож средних веков создавали с параметрами, соответствующими гармоническому правилу.

Золотое сечение в архитектуре

Множество построек древности, которые сохранились до сих пор, служат подтверждением тому, что архитекторы из эпохи средневековья были знакомы с гармоническим правилом. Очень хорошо заметно стремление соблюсти гармоническую пропорцию при сооружении церквей, значимых общественных зданий, резиденций королевских особ.

К примеру, собор Парижской Богоматери возведен таким образом, что многие из его участков соотносится с правилом золотого сечения. Можно найти немало произведений архитектуры 18 века, которые были построены в согласии с этим правилом. Правило применяли и многие русские архитекторы. Среди них был и М. Казаков, который создавал проекты усадеб и жилых зданий. Он проектировал здание сената и Голицынскую больницу.

Естественно, дома с таким отношением частей возводили и до открытия правила золотого сечения. Например, к таким зданиям относится церковь Покрова на Нерли. Красота здания приобретает еще большую загадочность, если учесть, что здание покровской церкви было возведено в XVIII веке. Однако современный вид постройка приобрела после реставрации.

В трудах о золотом сечении упоминается, что в архитектуре восприятие объектов зависит от того, кто наблюдает. Пропорции, образованные при помощи золотого сечения, дают максимально спокойное соотношение частей строения относительно друг друга.

Ярким представителем из ряда строений, соответствующих универсальному правилу, является памятник архитектуры Парфенон, возведенный еще в пятом веке до н. э. Парфенон устроен с восьмью колоннами по меньшим фасадам и с семнадцатью – по большим. Храм возведен из благородного мрамора. Благодаря этому использование раскраски ограничено. Высота строения относится к его длине 0,618. Если разделить Парфенон по пропорциям золотого сечения, получатся определенные выступы фасада.

Все эти сооружения имеют одно сходство – гармоничность сочетания форм и отменное качество строительства. Это объясняется использованием гармонического правила.

Важность золотого сечения для человека

Архитектура древних построек и средневековых домов довольно интересна и для дизайнеров современности. Это объясняется такими причинами:

• Благодаря оригинальному оформлению домов можно не допустить надоевших штампов. Каждое такое здание является архитектурным шедевром.
• Массовое применение правила для украшения скульптур и статуй.
• Благодаря соблюдению гармонических пропорций взгляд притягивается к более важным деталям.

Сегодня психологи пришли к выводу, что принцип золотого сечения — не что иное, как человеческая реакция на определенное соотношение размеров и форм. В одном эксперименте группе испытуемых предложили согнуть бумажный лист таким образом, чтобы стороны получились с оптимальными пропорциями. В 85 результатах из 100 люди сгибали лист практически в точном соответствии с гармоническим правилом.

Как утверждают современные ученые, показатели золотого сечения относятся скорее к сфере психологии, нежели характеризуют закономерности физического мира. Это объясняет, почему к нему проявляется такой интерес со стороны мистификаторов. Однако при построении объектов согласно этому правилу человек воспринимает их более комфортно.

Использование золотого сечения в дизайне

Принципы использования универсальной пропорции все чаще используют при строительстве частных домов. Особое внимание уделяется соблюдению оптимальных пропорций конструкции. Немало внимания уделяют правильному распределению внимания внутри дома.

Современная интерпретация золотого сечения уже не относится лишь к правилам геометрии и формы. Сегодня принципу гармонических пропорций подчиняются не только размеры деталей фасада, площадь комнат или длины фронтонов, но и цветовая палитра, используемая при создании интерьера.

Соорудить гармоничное строение на модульном основании гораздо проще. Многие отделения и помещения в этом случае выполняются как отдельные блоки. Они проектируются в строгом соответствии с гармоническим правилом. Возвести здание как набор отдельных модулей, значительной проще, чем создавать единую коробку.

Многие фирмы, занимающиеся сооружением загородных домов, при создании проекта соблюдают гармоническое правило. Это позволяет создать у клиентов впечатление, что конструкция здания детально проработана. Такие дома обычно описывают, как наиболее гармоничные и комфортные в использовании. При оптимальном выборе площадей комнат жильцы психологически ощущают успокоение.

Если дом возведен без учета гармонических пропорций, можно создать планировку, которая будет по соотношению размеров стен приближена к показателю 1:1,61. Для этого в комнатах устанавливают дополнительные перегородки, или переставляют предметы мебели.

Аналогично меняют габариты дверей и окон таким образом, чтобы проем имел ширину, показатель которой меньше значения высоты в 1,61 раза.

Сложнее подбирать цветовые решения. В этом случае можно соблюдать упрощенное значение золотого сечения – 2/3. Основным цветовым фоном следует занять 60% пространства комнаты. Оттеняющий оттенок занимает 30% помещения. Оставшаяся площадь поверхностей закрашивается близкими друг к другу тонами, усиливающими восприятие выбранного цвета.

Внутренние стены комнат делят горизонтальной полосой. Ее располагают в 70 см от пола. Высота мебели должна находиться в гармоническом соотношении с высотой стен. Это правило относится и к распределению длин. К примеру, диван должен иметь габариты, которые бы оказались не меньше 2/3 длины простенка. Площадь помещения, которая занята предметами мебели, тоже должна иметь определенное значение. Она относится к общей площади всего помещения как 1:1,61.

Золотая пропорция сложно применима на практике ввиду наличия всего одного числа. Именно поэтому. Проектирую гармоничные строения, пользуются рядом чисел Фибоначчи. Благодаря этому обеспечивается разнообразие вариантов форм и пропорций деталей строения. Ряд чисел Фибоначчи также носит название золотого. Все значения строго соответствуют определенной математической зависимости.

Кроме ряда Фибоначчи, в современной архитектуре применяют и другой метод проектирования – принцип, заложенный французским архитектором Ле Корбюзье. При выборе этого способа отправной единицей измерения выступает рост владельца дома. Исходя из этого показателя рассчитывают размеры здания и внутренних помещений. Благодаря этому подходу дом получается не только гармоничным, но и приобретает индивидуальность.

Любой интерьер приобретет более завершенный вид, если в нем использовать карнизы. При использовании универсальных пропорций можно вычислить его размер. Оптимальными показателями являются 22,5, 14 и 8,5 см. Устанавливать карниз следует по правилам золотого сечения. Маленькая сторона декоративного элемента должна относиться к большей так, как относится к сложенным значениям двух сторон. Если большая сторона будет равна 14 см, то маленькую стоит сделать 8,5 см.

Придать помещению уюта можно путем деления стеновых поверхностей при помощи гипсовых зеркал. Если стена поделена бордюром, от оставшейся большей части стены следует отнять высоту карнизной планки. Для создания зеркала оптимальной длины от бордюра и карниза следует отступить одинаковое расстояние.

Заключение

Дома, построенные по принципу золотого сечения, действительно получаются очень удобными. Однако цена постройки таких строений довольно высока, поскольку стоимость стройматериалов ввиду нетипичных размеров увеличивается на 70%. Этот подход совершенно не нов, поскольку большинство домов прошлого века создавали исходя из параметров хозяев.

Благодаря использованию метода золотого сечения в строительстве и дизайне здания получаются не только комфортабельными, но и долговечными. Они выглядят гармонично и привлекательно. Интерьер тоже оформляют по универсальной пропорции. Это позволяет грамотно использовать пространство.

В таких комнатах человек ощущает себя максимально комфортно. Соорудить дом с использованием принципа золотого сечения можно самостоятельно. Главное – рассчитать нагрузки на элементы строения, и правильно выбрать материалы.

Метод золотого сечения используют в дизайне интерьера, размещая в комнате декоративные элементы определенных размеров. Это позволяет придать помещению уюта. Цветовые решения тоже выбирают в соответствии с универсальными гармоническими пропорциями.

В течение многих столетий золотое сечение является основой архитектуры, живописи и других искусств. Золотое сечение — это природная гармония, пропорциональность, найти которую можно в самых разных живых структурах — в рисунке волокон дерева, в расположении лепестков цветов, в строении раковин и человеческого тела. Именно поэтому с самых древних времен человечество стремится использовать эту гармонию в повседневной жизни, в том числе и в строительстве.

Само понятие золотого сечения было введено греческим философом Пифагором, который сумел вывести формулу так называемой «божественной» пропорции. Он определил ее, как деление целого на две неравные части, при этом меньшая часть относится к большей точно так же, как большая к общему целому. Если за целое будет взята единица, то большая ее часть будет составлять 0,618, а меньшая — 0,382. Именно эти цифры можно использовать при проектировании домов по золотому сечению.

Как использовать золотое сечение в строительстве?

Все важные особенности будущего здания должны быть заложены в него еще на стадиях проектирования. Планирование строительства по золотому сечению начинается с определения главного модуля здания, который будет выступать условной единицей. Именно к нему впоследствии будут привязаны все остальные размеры объекта, и с его учетом будет разделяться внутреннее пространство объекта на секции.

В качестве модуля, важнейшей величины будущего строения можно взять средний человеческий рост или число, примерно соответствующее росту будущего собственника. Таким образом, владелец сможет спланировать строительство объекта, который будет максимально соответствовать ему самому.

Остальные выполняемые проектные и строительные работы будут зависеть от того, какую именно цель преследует собственник. Правило золотого сечения можно использовать не только при строительстве объектов, но также при проектировании отделки домов внутри и снаружи.

Где можно использовать золотое сечение?

Желая построить максимально функциональный и привлекательный жилой дом, собственник может использовать правило золотого сечения при определении соотношения цветов для оформления фасада или облицовки внутренних помещений. Учитывая это правило становится понятным, что для оформления комнаты или всего здания нужно будет использовать два цвета, причем, один из них будет доминирующим, занимающим около 60% всего оформляемого пространства, а второй — сопровождающим, занимающим от 30% до 40%. В интерьер можно также ввести и дополнительный цвет, которого должно быть не более 10%, его можно использовать для того, чтобы подчеркивать отдельные элементы декора или конструктивные детали здания.

Что касается самих цветов, то их выбирают с учетом стиля архитектуры и дизайна. Основной, сопровождающий и дополнительный цвета не обязательно должны сильно отличаться друг от друга. Иногда для оформления комнат можно использовать несколько оттенков одного цвета, делая мягкие переходы тональности и добиваясь, таким образом, нужного визуального эффекта.

Правило золотого сечения можно использовать и при создании общей дизайнерской композиции внешней или внутренней отделки. В этом случае выбирается главная деталь композиции, важнейшая фокусная точка освещения, меблировки и декора. Окружающее пространство заполняется аккомпанирующими элементами, которые подчеркивают выбранный стиль, главные конструктивные или дизайнерские решения. Опытные дизайнеры знают, что в любом интерьере должна быть динамика и развитие. Одноцветные и однородные дома не привлекают внимания, выглядят серо и совершенно не интересно.

Можно использовать золотое сечение и при делении стен на уровни. Для этого можно применять различные физические элементы, к примеру плинтуса. Если собственник хочет выполнить деление мягко и менее заметно, то стену можно оставить единым целым, применив принцип золотого сечения в расстановке мебели или в развеске панно. При таком способе оформления интерьера лучше использовать максимально нейтральный основной цвет, выставив на первый план яркие пятна декоративных элементов и всевозможных украшений.

Очень важно при оформлении здания выдержать правильное соотношение мебели и доступного пространства. С учетом правила золотого сечения, мебель в каждой комнате должна занимать не более 60% от общей композиции, иначе помещения будут выглядеть тесными и захламленными. До максимума повысить привлекательность и гармоничность внутренних помещений можно за счет проектирования мебели на заказ. В этом случае собственник сможет с учетом правила золотого сечения определить размеры и характеристики каждого отдельного элемента интерьера.

Правило 2/3 можно использовать практически при решении каждого вопроса, касающегося оформления комнат жилого дома. Так, при выборе подвесного светильника нужно учитывать, что он должен располагаться на высоте около 2/3 от высоты комнаты, диван должен занимать не больше 2/3 от выделенного под него простенка, журнальный столик должен быть больше 2/3 от размеров дивана, рядом с которым он располагается.

Правило золотого сечения можно использовать при проектировании придомовых территорий многоквартирных домов и частных строений, однако такие работы являются чрезвычайно сложными в выполнении, из-за чего к их реализации рекомендуется привлекать опытных проектировщиков. Для определения стоимости услуг специалистов можно воспользоваться калькулятором.

Золотое сечение в дизайне

Говорят, что “божественная пропорция” заложена в природе, и во многих вещах вокруг нас. Вы можете найти ее в цветах, ульях, морских раковинах, и даже нашем теле.

Эта божественная пропорция, также известная как золотое сечение, божественное сечение, или золотая пропорция может быть применена к различным видам искусства и обучения. Ученые утверждают, что чем ближе объект к золотому сечению, тем лучше человеческий мозг воспринимает его.

С тех пор как это соотношение было открыто, многие художники и архитекторы применяли его в своих работах. Вы можете найти золотое сечение в нескольких шедеврах эпохи Возрождения, архитектуре, живописи, и многом другом. В результате – красивый и эстетически приятный шедевр.

Немногие знают, в чем заключается тайна золотого сечения, что так радует наши глаза. Многие полагают, что то, что она появляется везде и является “универсальной” пропорцией, заставляет нас принять ее как что-то логическое, гармоничное и органичное. Другими словами, оно просто “чувствует” то, что нам нужно.

Итак, что такое золотое сечение?

Золотое сечение, также известное как “фи” по-гречески, это математическая константа. Оно может быть выражено уравнением a/b=a+b/a=1,618033987, где a больше, чем b. Это также можно объяснить последовательностью Фибоначчи, другой божественной пропорцией. Последовательность Фибоначчи начинается с 1 (некоторые говорят с 0) и добавляет к нему предыдущее число, чтобы получить последующее (т.е. 1, 1, 2, 3, 5, 8, 13, 21 …)

Если вы попытаетесь найти частное от деления двух последующих чисел Фибоначчи (т.е. 8/5 или 5/3), результат очень близок к золотому сечению 1,6 или φ (фи).

Золотая спираль создается с помощью золотого прямоугольника. Если у вас есть прямоугольник из квадратов 1, 1, 2, 3, 5 и 8 соответственно, как показано на рисунке выше, вы можете приступить к строительству золотого прямоугольника. Используя сторону квадрата, как радиус, вы создаете дугу, которая касается точек квадрата по диагонали. Повторите эту процедуру с каждым квадратом в золотом треугольнике, и в конечном итоге вы получите золотую спираль.

Где мы можем увидеть его в природе

Золотое сечение и последовательность Фибоначчи можно найти в лепестках цветов. У большинства цветков количество лепестков сводится к двум, трем, пяти или больше, что походит на золотое сечение. Например, у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34. Вероятно, семена цветков также следуют золотому сечению. Например, семена подсолнечника прорастают из центра и растут к внешней стороне, заполняя головку семени. Обычно они спиралевидные и имеют сходство с золотой спиралью. Более того, количество семян, как правило, сводится к числам Фибоначчи.

Руки и пальцы также являются примером золотого сечения. Посмотрите ближе! Основание ладони и кончик пальца разделен частями (костьми). Соотношение одной части в сравнении к другой всегда 1,618! Даже предплечья с руками находятся в таком же соотношении. И пальцы, и лицо, и можно продолжать список…

Применение в искусстве и архитектуре

Парфенон в Греции, как утверждается, был построен с использованием золотых пропорций. Считается, что размерные соотношения высоты, ширины, колонн, расстояния между столбами, и даже размер портика близки к золотому сечению. Это возможно потому, что здание выглядит пропорционально идеально, и оно было таким с древних времен.

Леонардо Да Винчи был также поклонником золотого сечения (и многих других любопытных предметов, собственно говоря!). Дивная красота Мона Лизы может быть связана с тем, что ее лицо и тело представляют собой золотое сечение, как и реальные человеческие лица в жизни. Кроме того, цифры в картине “Тайная вечеря” Леонардо Да Винчи расположены в порядке, который используется в золотом сечении. Если начертить золотые прямоугольники на холсте, Иисус окажется как раз в центральной доле.

Применение в дизайне логотипов

Неудивительно, что вы также можете найти использование золотого сечения во многих современных проектах, в частности, дизайне. Сейчас давайте сосредоточимся на том, как это может быть использовано в дизайне логотипа. Во-первых, рассмотрим некоторые из самых известных в мире брендов, которые использовали золотое сечение для совершенствования своих логотипов.

Видимо, Apple использовал круги из чисел Фибоначчи, соединив и обрезав формы для получения логотипа Apple. Неизвестно, было ли это сделано намеренно или нет. Тем не менее, в результате получился идеальный и визуально эстетичный дизайн логотипа.

Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения.

Логотип Pepsi создан двумя пересекающимися кругами, один больше другого. Как показано на рисунке выше, больший круг пропорционален в соотношении к меньшему – вы уже догадались! Их последний нерельефный логотип – простой, эффектный и красивый!

Кроме Toyota и Apple, логотипы некоторых других компаний, таких как, BP, iCloud, Twitter, и Grupo Boticario, как полагают, также использовали золотое сечение. И мы все знаем, насколько известны эти логотипы – все потому, что изображение сразу всплывает в памяти!

Как вы можете применить его в своих проектах?

Создайте эскиз золотого прямоугольника, как показано выше желтым цветом. Этого можно достичь путем построения квадратов с высотой и шириной из чисел, принадлежащих золотому сечению. Начните с одного блока и поместите другой рядом с ним. А другой квадрат, чья площадь равна тем двум, поместите над ними. Вы автоматически получите сторону из 3 блоков. После построения этой конструкции из трех блоков, в конечном итоге у вас будет сторона из 5 четырехугольников, из которой можно сделать другую (площадью в 5 блоков) коробку. Это может продолжаться сколько угодно, пока вы не найдете тот размер, который вам нужен!

Прямоугольник может перемещаться в любом направлении. Выделите мелкие прямоугольники и используйте каждый из них, чтобы собрать макет, который будет служить в качестве сетки дизайна логотипа.

Если логотип более округлый, то вам потребуется круговая версия золотого прямоугольника. Вы можете добиться этого начертанием кругов, пропорциональных числам Фибоначчи. Создайте золотой прямоугольник, используя только круги (это означает, что самый большой круг будет иметь диаметр 8, а у круга поменьше будет диаметр 5, и так далее). Теперь разделите эти круги и разместите их так, чтобы вы могли сформировать основную схему для вашего логотипа. Вот пример логотипа Twitter:

Примечание: Вам не обязательно чертить все круги или прямоугольники золотого сечения. Вы также можете использовать один размер неоднократно.

Как применять его в дизайне текста

Это проще, чем проектирование логотипа. Простое правило для применения золотого сечения в тексте заключается в том, что последующий больший или меньший текст должен соответствовать Фи. Давайте разберем этот пример:

Если размер моего шрифта – 11, то подзаголовок должен быть написан в более крупном шрифте. Умножаю шрифт текста на число золотого сечения, чтобы получить большее число (11*1,6=17). Значит подзаголовок должен быть написан в 17 размере шрифта. А теперь заголовок или название. Умножу подзаголовок на пропорцию и получу 27 (1*1,6=27). Вот так! Ваш текст теперь пропорционален золотому сечению.

Как применить его в веб-дизайне

А здесь немного сложнее. Вы можете оставаться верными золотому сечению даже в веб-дизайне. Если вы опытный веб-дизайнер, вы уже догадались, где и как ее можно применить. Да, мы можем эффективно использовать золотое сечение и применить его к сеткам наших веб-страниц и макетам пользовательского интерфейса.

Возьмите общее число сетки пикселей за ширину или высоту и используйте его для построения золотого прямоугольника. Разделите наибольшую ширину или длину для получения меньших чисел. Это может быть шириной или высотой вашего основного контента. То, что осталось, может быть боковой панелью (или нижней панелью, если вы применили его к высоте). Теперь продолжайте использовать золотой прямоугольник для дальнейшего применения его к окнам, кнопкам, панелям, изображениям и тексту. Вы также можете построить полную сетку, основанную на маленьких версиях золотого прямоугольника расположенных как горизонтально, так и вертикально для создания более маленьких объектов интерфейса, которые пропорциональны золотому прямоугольнику. Для получения пропорций вы можете использовать этот калькулятор.

Спираль

Вы также можете использовать золотую спираль, чтобы определить, где разместить контент на вашем сайте. Если ваша домашняя страница загружается с графическим контентом, как, например, на веб-сайте онлайн магазина или блога фотографий, вы можете воспользоваться золотым методом спирали, который используют многие художники в своих работах. Задумка в том, чтобы поместить наиболее ценный контент в центре спирали.

Контент со сгруппированным материалом тоже может быть размещен при помощи золотого прямоугольника. Это означает, что чем ближе спираль движется к центральным квадратам (к одному квадратному блоку), тем “плотнее” там содержимое.

Вы можете использовать эту технику, чтобы обозначить расположение вашего заголовка, изображений, меню, панели инструментов, окна поиска и других элементов. Twitter славится не только использованием золотого прямоугольника в дизайн логотипа, но и задействовал его в веб-дизайне. Как? Благодаря использованию золотого прямоугольника, или, другими словами концепцией золотой спирали, в странице профиля пользователей.

Но нелегко будет проделать такое на платформах CMS, где автор материала определяет расположение вместо веб-дизайнера. Золотое сечение подходит WordPress и другим дизайнам блога. Это, вероятно, потому, что боковая панель почти всегда присутствует в дизайне блога, который хорошо вписывается в золотой прямоугольник.

Правило третей

Для тех, кто не очень понимает язык математики, есть более простой способ. Он известен как правило третей. Оно не включает в себя точные математические вычисления, но помогает достигнуть правильных пропорций.

Все, что требуется – это разделить первоначальный эскиз на девять равных частей: 

Точки, где встречаются линии в сетке, будут основными точками вашего дизайна, от которых вы будете в дальнейшем отталкиваться. Вы можете поместить ключевую тему или основные элементы на одну или все точки пересечения. Фотографы также используют эту концепцию.

Если Вы разделите каждую колонку в сетке так, чтобы получились две равные половины, то Вы получите сетку для работы с дизайном сайта. Например, Вы можете разместить эмблему или логотип в верхнем правом квадрате в левой части. Менее важная информация, которая будет располагаться вертикально сверху вниз, может брать свое начало верхнем правом квадрате.

Чем ближе прямоугольники к соотношению 1:1,6, тем приятнее воспринимается картина человеческим мозгом (так как это ближе к золотому сечению). Если вы не любите математику и не хотите считать, то достаточно использовать отношение 3:5 при расчете золотого отношения. Результат будет не таким точным, но он будет близок к пропорциям, которые применяются в работе с дизайном.

Пример того, как можно использовать сечение в веб-дизайне, описан ниже. 

Золотое сечение на примере

Ширина вашего макета может быть фиксированная или гибкая, но прежде чем применить золотое отношение, вам нужно определить число, чтобы начать с ним работать. Для веб-дизайна это число будет равно числу пикселей в ширине лэйаута.

Если вы, например, работаете на лэйауте в 1200 пикселей, то нужно разделить это число на Phi. Для упрощения задачи, число Phi можно сократить до 1.62. При делении 1200 на 1.62, Вы получаете ширину основной колонны, что в нашем случае составит 740 пикселей.

Чтобы определить ширину второй колонки, просто вычтите ширину главной колонки от общей ширины. В этом примере получается 460 пикселей.

Теперь у вас есть две колонки в 740 пикселей и 460. При помощи этого простого вычисления, вы всегда сможете определить идеальные пропорции для колонок вашего сайта.

Для гибкого лэйаута нужно брать расчеты в процентах. Делим 100% на 1.62 и получаем основную колонку, которая займет 62%, а вторая – 38% соответственно. Далее вы сможете работать исходя из этого соотношения.

Золотое отношение может эффективно использоваться, при создании маленьких прямоугольников в пределах общего дизайна. Это пространство может быть использовано для кнопок навигации, заголовков изображений, пространства для объявлений или для текста, который располагается вокруг изображения. Как бы их не использовали, эти мини золотые прямоугольники будут пропорциональны и законченный вид дизайна, будет приятным завершением работы.

Золотое сечение – не панацея

Использование золотого сечения в дизайне не гарантирует успех вашего лендинга.

В то же время изображения, блоки текста и врезок могут быть хорошо представлены в маленьких золотых прямоугольниках, которые формируют красивый, сбалансированный вид, но число прямоугольников на каждой странице должно быть ограниченным. Ничто в веб-дизайне не должно быть в слишком большом количестве.

Также важно помнить о том, что есть много других факторов, которые нужно учитывать при создании дизайна, и которые будут соответствовать общей цели проекта.

Инструменты для дизайнеров

Калькулятор Phi

Когда вы вводите число в этот веб-инструмент, он рассчитывает результат, необходимый для золотого сечения. Этот сервис бесплатный и очень простой в использовании.

Типографический калькулятор Pearsonified

Это онлайн инструмент с кнопкой ‘Set My Type’. Вы просто нажимаете на нее после того, как введете ширину контента и/или размер шрифта, и сервис сам подберет лучшее типографическое решение. У Вас также есть возможность ввести значение CPL. Он оптимизирует размер знаков по линиям.

Сервис золотого отношения UX Triggers

Вы можете проверить любой сайт с помощью этого бесплатного сервиса и быстро определить использована ли последовательность Фибоначчи в дизайне.

Заключительные мысли

Веб-страницы выглядят более гармонично, когда они сделаны с использованием принципов золотого сечения. Это единственное соотношение, которое использовалось еще две тысячи лет назад, для тех же целей, что и сегодня. Посетителя интуитивно будут чувствовать комфорт гармоничного интерфейса, потому что им уже знакомы классические пропорции архитектурных строений и других произведений искусства.

Использование золотых прямоугольников дает чувство упорядоченности вашему лендингу. Но вы должны быть аккуратны, и избегать злоупотребления ими. Слишком большое их количество произведет обратный эффект и сделает дизайн приторным и менее привлекательным.

Сочетание математических вычислений и органической структуры в веб-дизайне может дать отличный результат. Необязательно, чтобы весь дизайн опирался на все упомянутые принципы, иногда достаточно правила третей, которое поможет вам правильно соблюсти пропорции и расположить элементы на свои места.

Готовы проверить полученные знания на лендинге? Вы можете выбрать подходящий шаблон и настроить его под себя в конструкторе LPgenerator, или, если у вас нет времени разбираться в тонкостях лендостроения, но при этом вам нужна уникальная страница с гарантированно высокой конверсией, подать заявку на индивидуальный дизайн. 

Он будет выполнен с учетом всех ваших пожеланий, подчеркнет особенности оффера и позиционирование бренда, а еще — легко масштабируется по мере необходимости.

Высоких конверсий!

12-03-2016

Разметчик Фибоначчи

Разметчик Фибоначчи — это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе — может быть ужасным. Разметчик Фибоначчи — отличное подручное средство для проектирования красивых изделий.

К чёму всё это? Одна закономерность упомянута, но можно заметить и другую — деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат — 1,618 — проверьте, если не лень. С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.

Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей. Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.

Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать  для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.

Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:

Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента — Разметчика Фибоначчи:

Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т.е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:

Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.

Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:

Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.

Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.

Соотношение между соседними фалангами пальцев — это ∳ (фи) = 1,618, Соотношение между локтем и кистью — это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка — это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток — это опять-таки ∳ (фи) = 1,618:

Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:

Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.

Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:

При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:

Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:

В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого. Главное — соотношение всё то же — ∳ (фи) = 1,618.

В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour («Высокий парень» или «Помпадур»), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас — это Золотой прямоугольник, положение сужения («талии» шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:

Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое «круглое» и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета. Или наоборот. Быстро, просто и удобно.

Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом  Прямоугольнике. Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.

Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок. Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов. Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.

Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку — надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т.д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.

Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т.д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.

Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или  экономией средств. Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам. Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.

Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.

В статье использованы материалы главы «A Guide to Good Design» из книги «Practical Furniture Design», написанной Graham Blackburn — признанным мебельным мастером, популяризатором деревообработки и издателем.

Евгений Фукс

технический консультант
LeighJigs.ru
[email protected]

Золотое сечение пропорция в строительстве Киров

Золотое Сечение (Golden Ratio) это деление какой-либо величины в отношении 62 % и 38 % (Ф=1:1,618). 

Человек как стандарт “Золотой пропорции”

Как бы ни удивительно это звучало, но в те времена, когда отсутствовали приборы для пространственных измерений, мерой для предков нынешних славян являлся сам человек. Чтобы убедиться в этом, достаточно вспомнить многие из названий в славянской измерительной системе: локоть, пядь, маховая и косая сажень, пясть, стопа. Таким образом, использование подобных мер длины уже закладывало основу для “золотого” соответствия измеряемых объектов пропорциям человеческого тела. И неудивительно, что строения, возводимые по таким естественным принципам, представляли собой образцы гармонии с внешним миром и окружающей природой.

Некоторые из особенностей древнерусских саженей

Наиболее употребительной в архитектурном планировании в Древней Руси была система измерений посредством так называемых “саженей”, которых существовало великое множество. Различные местности пользовались своими саженями, что отражалось в их названиях: владимирские, московские, новгородские. Чем можно объяснить такое различие? Скорее всего, тем, что люди из различных областей и регионов зачастую отличались по своему росту, размерам и пропорциям тел. Мало того, многие мастера могли изобрести и пользоваться в работе различными персональными саженями, что вполне естественно – ведь любое строительство должно вестись под нужды конкретного владельца. Если человек подбирает одежду с учётом роста, размеров и формы тела, логичным будет придерживаться тех же принципов в строительстве и обустройстве жилища. Невысокий дом явно не подойдёт для великана, а низкорослому человеку совсем ни к чему высокие потолки. Худому человеку не нужен слишком широкий дверной проём, в то время как человеку с крупными габаритами он просто необходим. Соответствие размеров нуждам владельца обеспечивает слаженность, гармонию и уют.

Однако, как подтверждают различные исследования, древнерусские сажени не являлись соразмерными и кратными друг другу величинами. Именно поэтому многие специалисты считают их использование нерациональным и лишённым удобства, предпочитая прибегать к классическим эталонным единицам, таким как метр.

Однако, чем же объяснить столь широкую практику использования иррациональных мерил у наших предков? К сожалению, в современной официальной науке укоренилось строго материальное восприятие окружающей действительности, и в результате многие из подобных вопросов остаются без вразумительного ответа.

Окружающий нас мир полон многочисленных движений и процессов, далеко не каждый из которых способен увидеть человеческий глаз. Множество волн, колебаний, микроскопических вибраций каждый миг повсеместно пронизывают внешнее пространство. Это своеобразная “пульсация природы” – не только живой, но и неживой. И сказанное в полной мере относится к различным элементам человеческого жилища, будь то стены, пол или потолки. Микроскопические волновые движения, неуловимые даже для многих чувствительных приборов, непрерывно воздействуют на человеческий организм, что не может остаться без последствий для него. Как отмечают исследователи в данной сфере, в тех помещениях, которые построены на основе стандартной метрической системы, волны принимают однообразный, “стоячий” характер, вредно воздействуя на состояние здоровья человека. Организм сопротивляется постоянному и однотипному волновому воздействию, что ослабляет и утомляет его, способствуя истощению.

Секреты гармонии в доме

Не являясь соразмерными и кратными величинами, древнерусские сажени лишены строгой физической рациональности. Отсутствие кратности в расстояниях приводит к разбалансированности “стоячих” волновых колебаний. В то же время, слаженность пропорций жилища с пропорциями его обитателей сопровождается возникновением других волн, вибрирующих в унисон с микроскопическими колебаниями в человеческом организме. Именно такое помещение – наилучшее для проживания людей, и поэтому во многих старинных домах люди чувствуют себя комфортно и расслабленно, не понимая, что же является тому причиной.

Конечно, системы точных измерений имеют важнейшее значение и широкую сферу применения, в том числе и в строительстве, однако планировать соразмерность и пропорции на их основе не является хорошим вариантом.

Если же жилище уже построено, тогда улучшения его можно добиться посредством визуальной разбивки на части и помещения, соответствующие условиям “золотой пропорции”.

Использование этих принципов на практике оживит любое помещение, одновременно способствуя хорошему самочувствию и более комфортному и приятному внешнему виду жилища.

Мы будем рады видеть Вас в числе наших клиентов!

Строительство по Золотой пропорции от

Центра Загородного Строительства «Асгард» — это надёжное долгосрочное
сотрудничество на взаимовыгодных условиях с соблюдением всех условий договора. Присоединяйтесь к числу
признательных клиентов, уже наслаждающихся комфортным проживанием в своём загородном доме.

Остались вопросы? Получите бесплатную консультацию:

Записаться на консультацию

Золотое сечение как объяснение пропорций красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

1. Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
2. Соотношение высоты верхней и нижней губы будет 1,618.
3. Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
4. Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
5. Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
6. Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
7. Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

1. Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
2. В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
3. Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
4. Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Ищук Андрей Петрович
Врач-стоматолог ортопед

Золотое сечение: величайший миф дизайна

В мире искусства, архитектуры и дизайна золотое сечение заслужило огромную репутацию. Такие великие люди, как Ле Корбюзье и Сальвадор Дали, использовали это число в своей работе. Говорят, что Парфенон, пирамиды в Гизе, картины Микеланджело, Мона Лиза, даже логотип Apple — все это включает его.

Это чушь собачья. Добросовестность эстетики золотого сечения — это городская легенда, миф, дизайнерский единорог. Многие дизайнеры не используют его, а если и используют, то сильно недооценивают его важность.Также нет науки, которая бы действительно это подтверждала. Те, кто считает, что золотое сечение — это скрытая математика, стоящая за красотой, попадают в ловушку 150-летней афера.

Пользователь Flickr Себастьян Бертран

Что такое золотое сечение?

Впервые описанное в книге Евклида Elements 2300 лет назад, установленное определение таково: два объекта находятся в золотом сечении, если их соотношение совпадает с отношением их суммы к большей из двух величин. Значение, которое получается, обычно записывается как 1.6180. Самым известным применением золотого сечения является так называемый золотой прямоугольник, который можно разделить на идеальный квадрат, и прямоугольник меньшего размера, имеющий такое же соотношение сторон, что и прямоугольник, из которого он был вырезан. Вы можете применить эту теорию к большему количеству объектов, подобным же образом разделив их.

Золотое сечение всегда будет немного неправильным.

Проще говоря: если у вас есть два объекта (или один объект, который можно разделить на два объекта, например, золотой прямоугольник), и если после выполнения приведенных выше математических расчетов вы получите число 1.6180, обычно считается, что эти два объекта попадают в золотое сечение. Только вот проблема. Когда вы делаете математику, золотое сечение не получается равным 1,6180. Получается 1.6180339887… И десятичные дроби идут бесконечно.

«Строго говоря, в реальном мире невозможно, чтобы что-либо попало в золотое сечение, потому что это иррациональное число», — говорит Кейт Девлин, профессор математики Стэнфордского университета. Вы можете приблизиться к более стандартным соотношениям сторон.По словам Девлина, дисплей iPad 3: 2 или дисплей 16: 9 на вашем HDTV «плавают вокруг него». Но золотое сечение похоже на пи. Подобно тому, как невозможно найти идеальный круг в реальном мире, золотое сечение нельзя строго применять к любому объекту реального мира. Всегда будет немного не по себе.

Золотое сечение как эффект Моцарта

Конечно, педантично. Разве 1,6180 недостаточно? Да, вероятно, так оно и было бы, если бы было что-то, что научно подтверждало бы идею о том, что золотое сечение имеет какое-либо отношение к тому, почему мы находим определенные объекты, такие как Парфенон или Мона Лиза , эстетически приятными.

Но нет. Девлин говорит, что идея о том, что золотое сечение вообще имеет какое-либо отношение к эстетике, исходит в первую очередь от двух человек, один из которых был неправильно процитирован, а другой просто придумывал дерьмо.

Первым парнем был Лука Пачоли, монах-францисканец, который еще в 1509 году написал книгу под названием De Divina Proportione , названную в честь золотого сечения. Как ни странно, в своей книге Пачоли не выступал за теорию эстетики, основанную на золотом сечении, поскольку она должна применяться к искусству, архитектуре и дизайну: вместо этого он поддерживал Витрувианскую систему рациональных пропорций после римского архитектора I века. , Витрувий.Представление о золотом сечении было ошибочно приписано Пачоли в 1799 году, по словам Марио Ливио, парня, который буквально написал книгу о золотом сечении. Но Пачоли был близким другом Леонардо да Винчи, чьи работы снова стали популярными в 19 веке. Поскольку да Винчи иллюстрировал De Divina Proportione , вскоре стало известно, что сам Да Винчи использовал золотое сечение в качестве секретной математики в своих изысканно красивых картинах.

Один парень, который поверил, что это был Адольф Цейзинг.«Это тот парень, которого действительно хочется сжечь на костре за репутацию золотого сечения», — смеется Девлин. Цайзинг был немецким психологом, который утверждал, что золотое сечение — это универсальный закон, описывающий «красоту и завершенность в сферах как природы, так и искусства … который пронизывает как высший духовный идеал все структуры, формы и пропорции, космические или индивидуальные. , органические или неорганические, акустические или оптические ».

Он был многословным парнем. Единственная проблема с Цейзингом заключалась в том, что он видел закономерности там, где их не было.Например, Зейзинг утверждал, что золотое сечение можно применить к человеческому телу, взяв высоту от пупка до пальцев ног, а затем разделив ее на общий рост. По словам Девлина, это просто произвольные части тела, сведенные в формулу: «При измерении чего-либо столь сложного, как человеческое тело, легко найти примеры соотношений, которые очень близки к 1,6».

Я никогда не припомню, чтобы в моей работе использовалось золотое сечение.

Но неважно, выдумана она или нет.По словам Девлина, теории Цейзинга стали чрезвычайно популярными, «эквивалентом эффекта Моцарта XIX века», ссылаясь на веру в то, что прослушивание классической музыки улучшает ваш интеллект. И это никогда не уходило. В 20 веке знаменитый швейцарско-французский архитектор Ле Корбюзье основал свою модульную систему антропометрических пропорций на золотом сечении. Дали написал свой шедевр «Тайная вечеря » на холсте в форме золотого прямоугольника. Тем временем искусствоведы начали прочесывать великие замыслы истории, пытаясь задним числом применить золотое сечение к Стоунхенджу, Рембрандту, собору Шатр и Сёра.Связь между золотым сечением и красотой с тех пор является уткой в ​​мире искусства, архитектуры и дизайна.

Ян Йен через Yanko Design

Вы действительно не предпочитаете золотое сечение

В реальном мире люди не обязательно предпочитают золотое сечение.

Девлин рассказывает мне, что в рамках продолжающегося, неопубликованного упражнения в Стэнфорде, он работал с факультетом психологии университета, чтобы на протяжении многих лет спрашивать сотни студентов, какой прямоугольник им нравится больше всего.Он показывает студентам наборы прямоугольников, а затем просит их выбрать понравившийся. Если бы за идеей о том, что золотое сечение является ключом к красивой эстетике, стояла какая-то правда, ученики выбрали бы прямоугольник, ближайший к золотому. Но они этого не делают. Они выбирают, казалось бы, наугад. И если вы попросите их повторить упражнение, они выберут разные прямоугольники. «Это очень полезный способ показать новым студентам-психологам сложность человеческого восприятия», — говорит Девлин. И это вовсе не показывает, что золотое сечение более эстетично для людей.

Эксперименты Девлина — не единственные, которые показывают, что люди не предпочитают золотое сечение. Исследование, проведенное школой бизнеса Haas в Беркли, показало, что в среднем потребители предпочитают прямоугольники в диапазоне от 1,414 до 1,732. В ассортименте есть золотой прямоугольник, но его точные размеры не являются фаворитом.

Многие современные дизайнеры не думают, что это полезно.

Дизайнеры, с которыми мы говорили о золотом сечении, в любом случае не находят его очень полезным.

Ричард Мейер, легендарный архитектор Центра Гетти и Музея современного искусства Барселоны, признает, что когда он только начинал свою карьеру, у него был треугольник архитектора, который соответствовал золотому сечению, но он никогда не проектировал свои здания, сохраняя золотое сечение в уме. «Есть так много других чисел и формул, которые более важны при проектировании здания», — говорит он мне по телефону, имея в виду формулы, которые могут рассчитывать максимальный размер определенных пространств или те, которые могут определять нагрузку на конструкцию.

Есть так много других чисел и формул, которые более важны при проектировании здания.

Алиса Андрасек, дизайнер Biothing, онлайн-хранилища вычислительных проектов, соглашается. «В своей работе я никогда не припомню, чтобы использовалось золотое сечение», — пишет Андрасек в электронном письме. «Я могу представить себе вложение золотого сечения в различные системы в качестве дополнительной« изюминки », но я не могу представить, чтобы оно управляло всем дизайном, как это было исторически… это слишком упрощенно.

Джорджия Лупи из Accurat, итальянской дизайнерской и инновационной фирмы, говорит, что в лучшем случае золотое сечение так же важно для дизайнеров, как и любое другое композиционное правило, такое как правило третей: может быть, прекрасное практическое правило , но хороший дизайнер может отклонить его. «На практике я не знаю, сколько дизайнеров сознательно используют золотое сечение», — пишет она. «Я лично никогда не работал с ним, мы использовали его в своих проектах».

Из всех дизайнеров, с которыми мы говорили, промышленный дизайнер Ив Бехар из Fuseproject, пожалуй, лучше всех относится к золотому сечению.«Иногда я смотрю на золотое сечение, когда наблюдаю за пропорциями продуктов и графики, которые мы создаем, но это больше информативно, чем догматично», — говорит он мне. Даже тогда он никогда не намеревается создавать что-то с учетом золотого сечения. «Это важно как инструмент, но не как правило».

Даже дизайнеры, которые являются и одновременно математиками, скептически относятся к использованию золотого сечения в дизайне. Эдмунд Харрис — доцент кафедры математики Университета Арканзаса, который использует множество формул для создания новых произведений искусства.Но Харрис говорит, что золотое сечение — это, в лучшем случае, лишь один из многих инструментов, имеющихся у математически склонного дизайнера. «Это простое число во многих отношениях, и в результате оно действительно встречается в самых разных местах…» — сообщает мне Харрис по электронной почте. «[Но] это определенно не универсальная формула эстетической красоты».

Таинство Тайной вечери , 1955, Сальвадор Дали

Почему мифы не исчезли?

Если эстетические достоинства золотого сечения настолько неубедительны, почему же миф продолжает существовать?

Девлин говорит, что это просто.«Мы существа, которые генетически запрограммированы видеть закономерности и искать смысл», — говорит он. Не в нашей ДНК быть комфортно с произвольными вещами, такими как эстетика, поэтому мы пытаемся подкрепить их нашим часто ограниченным пониманием математики. Но большинство людей на самом деле не понимают математику или то, как даже простая формула, такая как золотое сечение, применима к сложной системе, поэтому мы не можем проверить себя на ошибки. «Люди думают, что видят золотое сечение вокруг себя, в мире природы и в объектах, которые они любят, но на самом деле они не могут это подтвердить», — говорит мне Девлин.«Они жертвы своего естественного желания найти смысл в структуре Вселенной, не имея математических навыков, чтобы сказать им, что модели, которые, по их мнению, они видят, являются иллюзорными». Если вы видите золотое сечение в своих любимых дизайнах, вы, вероятно, видите вещи.

φ Фибоначчи в искусстве и архитектуре ★ Фибоначчи

Картины, рисунки, портреты

Витрувианский человек Леонардо да Винчи

«Фи — это больше, чем непонятный термин из математики и физики.«Кажется, это влияет не только на дизайн и строительство, но и на наши эстетические предпочтения. Когда субъектов исследования (не математиков или физиков, знакомых с фи) просили просмотреть случайные лица, наиболее привлекательными всегда считались те, которые демонстрировали пропорции «золотого сечения» между шириной лица и шириной глаз, носа. , и брови ». Исследователи заключают, что «золотое сечение вызвало инстинктивную реакцию» (Hom).

Попытки создать идеальную модель гармонично развитого человеческого тела продолжались в эпоху Возрождения.Широко известна идеальная человеческая фигура, созданная Леонардо да Винчи (1452-1519). Его рисунок «Витрувианского человека», как говорят, иллюстрирует золотое сечение (Hom). Отношение стороны квадрата к радиусу круга соответствует значению Phi с отклонением всего 1,7 процента (Posamentier and Lehmann 257). На нем отчетливо видна «пятиугольная» или «пятикратная» симметрия, характерная для растений и животных (Стахов 43). Голова, две руки и две ноги мужчины расположены в виде пентаграммы, как если бы они были лучами пятиугольной звезды.Да Винчи основывал измерения своего идеального мужчины на пропорциях, описанных Витрувием (глава 1 Книги III) (Картрайт).

Мона Лиза Леонардо да Винчи

Леонардо да Винчи проиллюстрировал книгу францисканского монаха Фра Лука Пачоли (ок. 1445-1517) « De Divina Proportione » (1509), в которой последний назвал число Фи «Божественной пропорцией; ” Позже да Винчи назвал это sectio aurea или Золотое сечение . Многие полагают, что да Винчи «сознательно руководствовался этим великолепным соотношением» и использовал золотое сечение во всех (или большей части) своих работ (Posamentier and Lehmann 260).Некоторые утверждают, что он использовал его для определения всех пропорций в своей картине Тайная вечеря , «включая размеры стола и пропорции стен и фона». Золотое сечение также присутствует в его культовом портрете Моны Лизы. Считается, что многие другие известные художники использовали золотое сечение, в том числе Микеланджело ( Мадонна Дони ), Рафаэль ( Сикстинская Мадонна ), Рембрандт ( A Автопортрет ), Сера ( Circus Parade ) и Сальвадор. Дали ( Половина гигантской чашки, подвешенная с необъяснимым отростком длиной пять метров, ) (Posamentier and Lehmann; Hom).

Художники нечасто явно свидетельствуют о сознательном использовании чисел Фибоначчи в качестве основной структуры своей работы. Однако одним из таких художников является немец Руне Милдс (род. 1935), который объяснил, что ее работа под названием Evolution: Progression and Symmetry III и IV «подчиняется законам симметрии» в том смысле, что в «восходящей линии» последовательность треугольников генерируется с помощью знаменитого математического ряда Леонардо Пизано, называемого Фибоначчи »(Posamentier and Lehmann 266).

Фибоначчи в современной архитектуре

Влияние Фибоначчи остается широко распространенным в современной архитектуре, где сама последовательность стала характерной чертой дизайна. Дымовая труба электростанции в Турку, Финляндия, стала достопримечательностью центра города, потому что на ней показаны первые десять чисел последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34 и 55) в игривый дисплей ярких неоновых цифр высотой два метра. «Дымоход Фибоначчи» был создан в 1994 году итальянским художником Марио Мерцем как проект экологического искусства (Лобо).Это всего лишь одна из его многочисленных «концептуальных» работ, включающих последовательность Фибоначчи. Его «Неаполь Фибоначчи» (1970) «состоит из десяти фотографий фабричных рабочих, строящих числа Фибоначчи от одного человека до группы из пятидесяти пяти человек». Мерц использовал числа Фибоначчи, потому что его желанием было «протестовать против дегуманизированного, ориентированного на потребителя общества», создавая искусство, вдохновленное последовательностью, «которая лежит в основе многих моделей роста естественной жизни» (Livio 176).

Моле Антонеллиана

Первоначально планировалось использовать как еврейскую синагогу, Моле Антонеллиана (1863–1889) сегодня используется как музей кино; Пятиэтажное здание в Турине, Италия, считается самым высоким музеем в мире.Это также самое высокое кирпичное строение в Европе с самым высоким куполом. На одной стороне четырехугольного купола сегодня первые числа Фибоначчи подсвечиваются красными неоновыми огнями. Il Volo Dei Numeri (Полет чисел) (1998) был разработан Марио Мерцем («Фибоначчи — Полет»).

Le Modulor

Купить сейчас на Amazon

Подобно Фибоначчи до него, архитектор XX века Шарль-Эдуард Жаннере (известный как Ле Корбюзье) (1887–1965) во время путешествий увлекся математическими концепциями; он путешествовал по Европе и изучал принципы пропорции, исследуя древние здания везде, где бывал, особенно у немецких архитекторов (Коэн).Десятилетия спустя Ле Корбюзье опубликовал Le Modulor: Гармоничная мера в человеческом масштабе, универсально применимая к архитектуре и механике и настаивал на том, что его работа представляет собой уникальную универсальную измерительную систему, которая придаст архитектуре математический порядок, ориентированный на человеческий масштаб. «Ле Корбюзье разработал свою доктрину пропорций конструкции, объединив имперскую систему измерения на основе стопы с метрической десятичной системой и связав это с измерениями человеческого тела.Он начал с предполагаемого стандартного размера человеческого тела и обозначил три интервала, связанных друг с другом в пропорции золотого сечения »(« Ле Корбюзье »). В частности, он объяснил: «Человек с поднятой рукой обеспечивает основные точки смещения пространства — стопу, солнечное сплетение, голову и кончик пальца поднятой руки — три интервала, которые дают ряд участков, определяемых Фибоначчи» ( Posamentier and Lehmann 241). Это был «инструмент линейных или оптических измерений, подобный музыкальному сценарию», с которым он был знаком (Коэн).Его систематический «инструмент» для «планирования архитектуры и промышленных продуктов получил всемирное признание и применялся бесчисленным количеством практиков» («Ле Корбюзье»).

The Core

Построенный в форме подсолнуха и размером с космический корабль, Core был впервые построен в 2005 году и переосмыслен в 2017-2018 годах. Здание, в котором находится выставка «Невидимые миры» в Образовательном центре Корнуолла, было спроектировано с использованием естественных форм (биомимикрия) и устойчивой конструкции и моделей, основанных на числах Фибоначчи («Как»).Архитектор Джолион Брюис объясняет: «Мы решили, что структура самого здания должна быть получена из двойной спирали, и мы обратились к математике, лежащей в основе этих спиралей в природе, чтобы создать дизайн. Мы были рады обнаружить, что в результате получилась эффективная и элегантная сеть деревянных балок »(« Путешествие »9).

Современная фотография

Пейзажный фотограф из Сан-Франциско Майк Спинак рассказывает о некоторых из многих способов, которыми современные художники, в том числе фотографы, «извлекают большое количество математических построений из Золотого сечения для создания рекомендаций по композиции.Он говорит: Они делят отрезок в соответствии с ~ 1.618 (Золотое сечение). Они образуют прямоугольник, длинные стороны которого примерно в 1,618 раза длиннее коротких сторон (золотой прямоугольник). Они образуют равнобедренный треугольник, в котором две длинные стороны треугольника примерно в 1,618 раза длиннее короткой стороны (Золотой треугольник). Они образуют треугольник, в котором самая длинная сторона в ~ 1,618 раза длиннее второй по длине стороны, что в ~ 1,618 раза длиннее самой короткой стороны (треугольник Кеплера).Они образуют логарифмическую спираль, которая расширяется примерно в 1,618 раза на каждую четверть оборота своего вращения (Золотая спираль). И так далее, с множеством других, таких как золотой ромб, Седло Баккера, Крест Святого Андрея и Арматура прямоугольника Було. Некоторым художникам также нравятся более наклонные и эзотерические конструкции, такие как разделение видимого светового спектра на золотое сечение или его сегменты (Спинак).

Далласский фотограф Джеймс Брэндон предлагает несколько советов о том, как фотографы-любители могут использовать золотое сечение для создания фотографии.По словам Брэндона, в программе Adobe Lightroom 3 есть опция наложения Golden Ratio для обрезки изображения. Линии интереса или точки на фотографии выстраиваются так, чтобы они совпадали с сеткой золотого сечения. Если взять «золотую середину» соотношения Фибоначчи и продублировать ее четыре раза в сетку, то получится сетка по правилу третей. Однако при ближайшем рассмотрении становится очевидным, что сетка не разделяет раму точно на три части. Вместо сетки из 3 частей, разделяющей кадр 1 + 1 + 1, есть сетка, разделяющая кадр по вертикали и горизонтали 1+.618 + 1 (Брэндон). Популярный способ применить спираль Фибоначчи к композиции — расположить «основной элемент изображения примерно там, где плотно закрученный« конец »золотой спирали вписался бы в рамку». Фотография «считается еще более эстетичной», если объект изображения можно расположить так, чтобы «некоторые линии изображения примерно следовали линиям спирали». Различные другие конструкции, перечисленные Спинаком, иногда «используются для выбора относительных пропорций — таких как композиция с фоном здания ~ 1.На фото в 618 раз выше человека на переднем плане. Или их используют для подбора цветовых сочетаний палитры рисунка »(Спинак). Спинак говорит, что практика применения золотой середины к композиции «по-видимому, достигла уровня устоявшейся ортодоксальности». Он добавляет, что поиск в Google по этой теме «даст более полутора миллионов списков». Более того, «в большинстве базовых инструкций по фотографии композиция обсуждается с использованием золотой середины». Adobe Lightroom имеет «несколько встроенных в программу наложений золотого сечения», включая наложения для сетки золотого сечения, золотой спирали и креста Святого Андрея.Посетители других веб-сайтов могут видеть свои фотографии «с наложением на них« золотого сечения ». Существуют также программные приложения, позволяющие наложить что-либо на экран вашего компьютера с помощью различных визуальных конструкций, основанных на золотом сечении ». Наконец, суппорты золотого сечения можно приобрести в Интернете в сотнях источников.

Золотая середина популярна не только для сочинения, но и для анализа композиций. «Аналитики деконструируют изображения, рисуя различные линии и узор, накладываемые на изображения» и определяя, соответствует ли конкретное изображение некоторой производной от золотой середины (спинак) и насколько близко.

Брэндон настаивает: «Соотношение Фибоначчи — мощный инструмент для компоновки фотографий, и его не следует сбрасывать со счетов как незначительное отличие от правила третей. Хотя сетки выглядят одинаково, использование Фи может иногда означать разницу между фотографией, которая просто щелкает, и фотографией, которая кажется не совсем правильной ». Он считает Фи гораздо более совершенным инструментом композиции для использования «и [] гораздо более интеллектуальным и исторически доказанным методом создания сцены» (Брэндон).

Фракталы

Автор Джесс МакНалли описывает фракталы как «паттерны, образованные из хаотических уравнений [которые] содержат самоподобные паттерны сложности, возрастающей с увеличением.«Почти идентичные, но уменьшенные копии целого создаются, когда вы разделяете фрактальный узор на части. Дублируя или повторяя относительно простые уравнения, порождающие фракталы, образуется бесконечная сложность. Создаются уникальные, но узнаваемые узоры. Примечательно, что количество определенных геометрических фигур определенного размера, образованных в узорах, часто оказывается числами Фибоначчи! (МакНелли).

Сетка золотого сечения, Фибоначчи и многое другое

Область шрифта оказывает определенное влияние на печатный материал или макет экрана.Поэтому, когда вы начинаете свой дизайн, разумно уделить некоторое внимание области шрифта и принципам макета страницы. Далее мы объясним различные методы и представим бесплатные шаблоны для загрузки.

Макеты страниц могут принимать различные формы и стили: от роскошной брошюры, напечатанной на глянцевой художественной бумаге с большим количеством свободного места для рекламы роскошных ванных комнат, до еженедельного рекламного проспекта из вашего дисконтного супермаркета, до краев забитого текстом и фотографиями на недорогой газетной бумаге.

Воздействие дизайна зависит от многих аспектов, таких как цвет, текстура, изображения и типографика, а также количество пробелов внутри и снаружи макета.

Каждый макет основан на фоновом фрейме, который включает в себя текстовую область страницы или экрана. Эта область называется областью шрифта или областью печати и имеет большое влияние на то, как воспринимается дизайн — независимо от того, был ли он разработан намеренно или нет. Перед тем, как приступить к макету, вам следует подумать о размере и расположении области шрифта и области печати.

Обзор статьи

>>> Шаблоны областей свободного типа для загрузки <<<

Обзор методов построения страниц

• Золотое сечение
  Золотое сечение относится к классическому методу, восходящему к эпохе Возрождения . Золотое сечение можно использовать для определения пропорций рисунков и структур, а также для определения области шрифта или выбора размера бумаги. Числовая последовательность Фибоначчи тесно связана с золотым сечением.
• Построение линии (также: диагональное построение)
  Построение линии использует диагонали, которые на первый взгляд кажутся ужасно математическими. Но после некоторой практики этот метод станет хорошей альтернативой золотому сечению.
• Простая последовательность чисел
  Пропорции полей определяются с помощью числовой последовательности 2: 3: 4: 5 или 2: 3: 4: 6.
• Сетка 9 × 9
  Сетка 9 × 9 — еще одно эффективное средство быстрого и легкого достижения вашей цели.Однако результат нелегко масштабировать.

Основы построения страницы

Мы воспринимаем впечатление пространственной гармонии и баланса, когда под объектами больше свободного пространства, чем над объектами. Таким образом, воспринимаемый гармонический зрительный центр всегда немного выше расчетного. Мы учтем этот факт в каждом из типов конструкций.

Область шрифта на отдельной странице обычно располагается горизонтально по центру. Для многостраничных документов вы должны принять во внимание, что читатель также будет смотреть на две противоположные страницы, и, следовательно, свободное пространство внутри, так называемое внутреннее поле , имеет двойное влияние.Таким образом, внутреннее поле двусторонних документов всегда примерно в два раза меньше ширины внешнего поля. Также есть верхнее поле, то есть свободное пространство над областью печати, и нижнее поле у ​​нижнего края.

Поля и область шрифта

Построение страницы с использованием золотого сечения и Фибоначчи

Мы встречаем золотое сечение как правило пропорциональности в архитектуре, живописи, скульптуре и природе. Это помогает нам гармонично разделить площади и расстояния.Также соотношение между прописными и строчными буквами часто основывается на золотом сечении. Если линейный сегмент разделен на две длины таким образом, что отношение полной длины сегмента к большей длине равно отношению большей длины к меньшей длине, то сегмент был разделен на золотое сечение.

Последовательность Фибоначчи тесно связана с золотым сечением, и, чтобы упростить задачу, ее можно использовать для определения области типа на основе «божественных пропорций».Последовательность Фибоначчи — это 1, 1, 2, 3, 5, 8, 13, 21, 34 и т.д., так что каждое число является суммой двух предыдущих. Пример: 5, добавленное к предыдущим 3, равно 8.

Теперь давайте применим числовую последовательность к двустороннему макету страницы. Строго говоря, здесь он служит не для определения области шрифта, а для определения полей и результирующих пропорций пространства печати.

Внутреннее поле всегда наименьшее. После этого размер поля увеличивается по часовой стрелке для правой страницы и против часовой стрелки для левой страницы.Применяя числовую последовательность к размерам полей, мы получаем 2 единицы для внутреннего поля, 3 единицы для верхнего поля, 5 единиц для внешнего поля и 8 единиц для нижнего поля. Размер единиц может быть определен индивидуально в зависимости от количества контента, продукта и целевой аудитории.

Область шрифта в соответствии с золотым сечением

Область текста с использованием метода построения линий

В этом методе используются диагональные линии для создания области шрифта. Конечный размер варьируется при таком подходе.Сначала нарисуйте две диагональные линии на всем развороте, затем по одной диагонали на каждой странице от внешнего нижнего угла до внутреннего верхнего угла. Чтобы определить верхнюю левую начальную точку области шрифта, возьмите любую точку на правой диагонали одной страницы. Оттуда проведите горизонтальную линию вправо, пока не дойдете до полной диагонали разворота. Оттуда пройдите вниз по вертикали до диагонали одной страницы и оттуда проведите горизонтальную линию, чтобы завершить прямоугольник. Это может показаться запутанным, поэтому для пояснения взгляните на иллюстрацию ниже.

Вы можете изменить размер области шрифта в любое время, переместив верхнюю левую начальную точку на правой отдельной диагонали страницы дальше вверх или вниз. Переместите его вверх, чтобы увеличить область шрифта, сохраняя пропорции, и переместите вниз, чтобы уменьшить.

Введите область с использованием диагональных линий

План B

Если вам нужна помощь с размером, вы можете нарисовать дополнительную линию: после создания всех четырех диагональных линий начните вертикальную линию в точке, где диагональ одной страницы и диагональ полного разворота встретите и подтяните его к краю страницы.Оттуда начните еще одну линию, которая идет до точки пересечения другой страницы. Это создает новую точку пересечения между последней строкой и диагональю одной страницы — и это верхняя левая начальная точка для прямоугольника области шрифта.

Введите диагональ области

Построение страницы с использованием числовой последовательности

Числовые последовательности 2: 3: 4: 5 и 2: 3: 4: 6 можно использовать для простого определения размеров четырех полей. Однако этот метод не учитывает соотношение ширины и высоты бумаги.Тем не менее, использование двух числовых последовательностей дает быстрое, часто красивое решение.

Область ввода

Построение страницы с использованием сетки 9 × 9

Этот метод делит ширину и высоту страницы на девять равных квадратов. Теперь оставьте по одному квадрату вверху и у внутреннего края, соответственно, пустым и по два квадрата снаружи и внизу каждый. Недостатком этого метода является немасштабируемая ширина поля и относительно небольшой и, следовательно, фиксированный размер области шрифта.

Сетка 9 × 9

Сетка макета

Наша область шрифта, или, скорее, ширина полей, определяет внешние края.Но внутри область шрифта все еще пуста. Но нам также необходимо структурировать внутреннюю часть области шрифтов, особенно в случае сложных проектов со сложным содержанием и многостраничными документами. Поэтому мы используем сетку макета , чтобы помочь нам.

Сетка делит область шрифта по горизонтали и вертикали на модули, которые упрощают организацию текста и изображений.

Горизонтальное деление

Начнем с горизонтального деления. Он создается сеткой столбцов , которая делит текст на несколько столбцов плюс область между столбцами, желоб.В нашем примере мы используем бумагу шириной 200 мм и область шрифта с использованием диагональной конструкции. Размер результирующей области шрифта составляет

 161 x 224,5 мм. 

Ширина области шрифта разделена на три текстовых столбца шириной 50,3 мм и с отступом 5 мм.

Ячейки сетки в области шрифта

Вертикальное деление

В вертикальной ориентации высота области шрифта изначально определяет высоту столбца, которая должна быть кратна базовой сетке, то есть расстоянию между строками основного текста.Теперь мы разделим высоту, чтобы создать ячейки. Высота ячейки обычно определяется шириной ячейки для создания гармоничного горизонтального формата. Часто наименьший размер изображения используется для определения размера ячейки. Однако высота ячеек должна быть такой, чтобы несколько ячеек друг над другом заканчивались точно на нижнем краю области шрифта — поэтому высота области шрифта всегда кратна высоте ячейки сетки.

Ячейки сетки

Теперь ячейки заполняют всю область текста и упрощают размещение объектов и определение размеров.Например, изображения или блоки теперь перемещаются с шагом ячейки сетки. Наименьшее изображение или самый маленький прямоугольник имеют размер ячейки сетки. Большие изображения всегда кратны ячейкам сетки.

Пример макета статьи в текстовом пространстве с использованием ячеек сетки.

На практике можно сказать, что чем меньше размер ячейки, тем больше гибкость дизайна, но тем более хаотичным может стать расположение объектов. Если ячейки сетки слишком малы, сетка больше не используется.

Пример расчета типовой площади

Поясним это с помощью расчета типовой площади.Это также показывает, что не всегда можно произвести расчет с точностью до миллиметра. Лучше постараться сохранить гибкость области шрифта и сетки макета. Предположим следующее:

Размер бумаги : 200 x 280 мм
Основной текст : размер шрифта 9 пунктов, расстояние между строками 12 пунктов

Согласно черновикам области шрифта, описанным выше, наша запланированная высота области шрифта составляет приблизительно 210 до 230 мм. Используя метод построения линии , мы получили бы высоту области шрифта 225 мм.

Теперь разделим высоту 225 мм на 12 пунктов базовой сетки, то есть 4,236 мм, что равно 53,11. Но нам нужно точное кратное нашей базовой сетке. Итак, мы округляем до 53 строк и уменьшаем высоту области шрифта до 53 * 4,236 = 224,5 мм.

Если у нас есть 53 линии, идеальным вариантом будет 6 модулей сетки, каждый из которых содержит 8 строк плюс один ряд желоба. Следовательно, у нас есть 6 модулей сетки * 8 рядов = 48 линий плюс 5 рядов желоба = 53 линии = 224,5 мм.

Подведем краткий промежуточный вывод.Мы вычислили следующие значения для нашей страницы:

• Сетка : 6 модулей сетки по 8 строк каждый
• Раздел : 53 строки по 12 точек в каждой
• Эффективная высота области шрифта : 224,5 мм

Каков размер верхнего и нижнего поля? Это можно рассчитать следующим образом:
280 мм (высота бумаги) — 224,5 мм (высота области шрифта) = 55,5 мм остается для верхнего и нижнего поля.

Пропорции маржи согласно Фибоначчи : 55.5 мм / 8 x 5 = 34,7 мм для нижнего поля; 20,8 мм для верхнего поля; в качестве альтернативы мы берем пропорции полей линейной конструкции , которая дает 37,1 мм для нижнего поля и 18,4 мм для верхнего поля.

• Верхнее поле : 18,4 мм
• Нижнее поле : 37,1 мм

Расчет области шрифта

Создание сетки дизайна в InDesign

В Adobe InDesign область шрифта определяется путем ввода ширины поля .Значения можно вводить либо в начале при создании файла, либо позже при открытом файле.

Вы можете определить область типа в InDesign при создании документа …

Если вы вводите значения впоследствии, обратите внимание на то, какие страницы активны при открытии диалогового окна, потому что только поля открытых страниц будут изменены!

Чтобы установить все страницы документа, дважды щелкните A-Master на панели «Страницы», чтобы отобразить главную страницу и активировать вторую мастер-страницу в случае документа разворота.После этого откройте диалоговое окно, чтобы ввести поля через Макет> Поля и столбцы.

… но это можно сделать и на более позднем этапе.

Создание сетки в InDesign

Модули сетки можно создавать с помощью линий сетки. Как вариант, создайте светлые прямоугольники, поместите их на отдельный слой и заблокируйте их. Вы можете показывать эти прямоугольники каждый раз, когда вам нужна помощь в позиционировании элементов, и скрывать их при предварительном просмотре.

Особые случаи

Существуют определенные обстоятельства, при которых область типа и сетка проекта должны соответствовать определенным спецификациям.Обычно это происходит, если части контента содержат фиксированные измерения, как в случае с рекламой. Клиент покупает рекламу определенной ширины и высоты, которую дизайнер должен интегрировать в область шрифта. В идеале наименьший размер объявления идентичен ячейке сетки, а более крупный размер рекламы соответствует нескольким ячейкам сетки. Однако на практике часто бывает наоборот, и ячейки сетки должны соответствовать пропорциям высоты и ширины объявления.

• Перед созданием области шрифта и сетки дизайна проверьте возможные размеры объявлений.
• Пропорции ячейки сетки не обязательно должны совпадать с пропорциями объявления. Квадратная реклама, например, также может состоять из модулей сетки 2 x 3.
• Если сомневаетесь, используйте небольшие ячейки сетки для большей гибкости.

Шаблоны текстовой области

Разметка текстовой области — непростая задача, особенно для новичков. Поэтому мы создали несколько шаблонов для всех типов расчетов в виде файла InDesign, который вы можете бесплатно скачать здесь. Основные данные:

• A4
• 200 x 280 мм
• двух размеров в зависимости от области типа

Загрузки

Шаблоны области типа золотого сечения:

Загрузить шаблон области шрифта A4

Загрузить 200 x Шаблон области шрифта 280 мм

Шаблоны области типа построения диагонали / линии:

Загрузить шаблон области шрифта A4

Загрузить шаблон области шрифта 200 x 280 мм

Шаблоны области типа номерной серии:

Загрузить область шрифта A4 template

Загрузить шаблон области шрифта 200 x 280 мм

Модульные шаблоны сетки 9 × 9:

Загрузить шаблон области шрифта A4

Загрузить шаблон области шрифта 200 x 280 мм

Кредиты: Rawpixel.com / Shutterstock.com

geometry — Новая очень простая конструкция золотого сечения, включающая треугольник, квадрат и пятиугольник со сторонами одинаковой длины. Есть ли предшествующий уровень техники?

Перенос моих мыслей из комментариев под моим ответом на другой вопрос …

Квадрат и треугольник здесь не имеют ничего общего с проявлением золотого сечения. Суть конструкции такова:

У фигуры есть две основные характеристики:

1. $ O $ лежит на серединном перпендикуляре ребра $ \ overline {RS} $ правильного пятиугольника; и,
2. $ B $ лежит на перпендикуляре к $ \ overline {RS} $ через $ S $.

Эта информация — все, что нам нужно , чтобы найти $ \ phi $.

Так как $ \ треугольник OAM \ sim \ треугольник OBN $, имеем
$$ \ frac {a} {b} = \ frac {\ frac {1} {2} | \ overline {AQ} |} {\ frac {1} {2} | \ overline {RS} |} = \ frac {\ text {диагональ правильного пятиугольника}} {\ text {край правильного пятиугольника}} = \ phi = 1.618 \ dots $$

(используя хорошо известное свойство правильных пятиугольников), а затем золотистость отношения $ a / b $ переходит к целевому соотношению $ b / (a-b) $, потому что именно так работает золотое сечение.:) $ \ qquad \ square $

Как я пишу в своих ссылках на комментарии:

$$ \ text {[Эта] конструкция — это} \ textit {подлый} \ text {, в том смысле, что она заставляет думать} \\ \ text {, что квадрат и треугольник имеют значение, хотя на самом деле это не так.} $$

Конечно, четность и нечетность подсчетов соответствующих ребер квадрата и треугольника естественным образом гарантируют, что целевой сегмент имеет конечную точку на серединном перпендикуляре согласно «характерной характеристике» $ (1) $; и наличие квадрата подходящего размера и положения делает перпендикуляр в $ (2) $ естественной частью конструкции.(Плюс, как упоминает OP, прогрессия от 3 до 4 — 5 долларов имеет некоторую привлекательность. Я также скажу, что мне нравится скрытый аспект . 🙂 Кроме того, ничего не говорится о конкретной геометрии этих элементов. в игру: треугольник может быть просто равнобедренным; квадрат мог быть просто прямоугольным; и / или любое количество дополнительных фигур может присоединиться к ним (или заменить их) в цепочке. Это не имеет значения; , пока выполняются $ (1) $ и $ (2) $, конструкция дает золотое сечение.

Например, вот сравнительно хитрая конструкция, которая может создать (ложное) впечатление, что прогрессия на $ 5 $ — $ 6 $ — $ 7 $ в количестве ребер компонентов имеет особую связь с $ \ phi $:

Золотое сечение источника

D | Геометрия в дизайне

Золотое сечение:
Детали золотого сечения объясняются в следующих пунктах:
1. Историческая справка
2. Золотое сечение
3. Построение золотого прямоугольника
4.Примеры золотого сечения

1. Историческая справка:
В математике и искусстве две величины находятся в золотом сечении, если отношение суммы величин к большему количеству равно отношению большего количества к меньшему. Выражается алгебраически:

, где греческая буква фи () представляет собой золотое сечение. Его значение:

Золотое сечение, или фи, было впервые понято и использовано древними математиками в Египте две-три тысячи лет назад из-за его частого использования в геометрии.Фидий (500 г. до н. Э. — 432 г. до н. Э.), Греческий скульптор и математик, изучал Фи и использовал его во многих проектах своих скульптур, таких как статуя богини Афины в Афине и состояние бога Зевса в Олимпиаде. В Elements , самом влиятельном учебнике математики из когда-либо написанных, Евклид Александрийский (ок. 300 г. до н.э.) определяет пропорцию, полученную в результате деления линии на то, что он называет ее «крайним и средним соотношением». Определение Евклида гласит:

Прямая линия, как говорят, была разрезана в крайнем и среднем соотношении, когда, как целая линия относится к большему сегменту, тем больше и меньше к меньшему.

Другими словами, на диаграмме ниже точка C делит линию таким образом, что отношение AC к CB равно отношению AB к AC .

Название « Золотое сечение » появляется в области раздела формы (Золотое сечение по-гречески) Леонардо да Винчи (1452-1519), который использовал это золотое сечение во многих своих шедеврах, таких как Тайная вечеря и Мона Лиза.

В 1900-х годах математик из Мексики по имени Марк Барр представил золотое сечение с помощью греческого символа Φ (фи).

2. Золотое сечение:
Золотое сечение получается делением любого члена последовательности Фибоначчи на его предыдущее число. Оно имеет значение, приблизительно равное 1,618, и также известно как золотое сечение, золотая середина, крайнее и среднее отношение, медиальное сечение, божественная пропорция, божественное сечение, золотая пропорция, золотая срезка, золотое число, среднее Фидия и т. Д.

Геометрическая спираль и геометрический прямоугольник — две наиболее важные конструкции, полученные из золотого сечения.Золотой прямоугольник имеет высоту и ширину в золотом сечении, тогда как золотая спираль — это логарифмическая спираль, коэффициент роста которой является золотым сечением. Другие важные конструкции — золотой треугольник и золотой эллипс. Золотой треугольник представляет собой равнобедренный треугольник с углом при вершине 36 градусов и углами основания, равными 72 градуса каждый.

3. Построение золотого прямоугольника:
• 3a — Использование метода построения квадрата
• 3b — Использование метода построения треугольника

• 3а.Использование метода построения квадрата:

1. Нарисуйте квадрат

2. Проведите диагональ от средней точки A одной из сторон до противоположного угла B. С центром A нарисуйте дугу, чтобы разрезать сторону в C. Нарисуйте перпендикуляр от C, чтобы получить золотой прямоугольник.

3. Золотой прямоугольник можно разделить, как показано. При подразделении он производит пропорциональный золотой прямоугольник меньшего размера, называемый обратным, а квадратная область, называемая гномоном, остается после подразделения.

4. Процесс подразделения может продолжаться, создавая более мелкие пропорциональные прямоугольники и квадраты.

5. Пропорционально уменьшающиеся квадраты могут дополнительно образовывать спираль, используя радиус, равный длине сторон квадрата.

6. Квадраты из раздела золотого сечения также находятся в золотой пропорции друг к другу.

• 3б. Использование метода построения треугольника:

1. Нарисуйте прямоугольный треугольник, стороны которого имеют соотношение 1: 2.Используя D в качестве центра и DA в качестве радиуса, нарисуйте дугу, которая пересекает гипотенузу в точке E.

2. С центром C в качестве центра и радиусом CE нарисуйте еще одну дугу, которая пересекает переменный ток в точке B.

3. Из точки B, нарисуйте перпендикуляр к DC.

4. AB и BC имеют золотые пропорции, и деление треугольника дает стороны прямоугольника в золотой пропорции.

Помимо золотого прямоугольника, метод построения треугольника создает серию кругов и квадратов, которые пропорциональны друг другу в золотом сечении.

Помимо золотого прямоугольника, метод построения треугольника создает серию кругов и квадратов, которые пропорциональны друг другу в золотом сечении.

4. Примеры золотого сечения:
• 4a — В природе
• 4b — В человеческом теле
• 4c — В искусстве и архитектуре
• 4d — В музыке

• 4a. In Nature:
Если посмотреть на ряд семян в центре подсолнечника, он может заметить что-то, похожее на спиральные узоры, изгибающиеся влево и вправо.Удивительно, но после подсчета этих спиралей общая сумма будет числом Фибоначчи. Разделив спирали на те, которые направлены влево и вправо, мы получим два последовательных числа Фибоначчи. Таким образом можно расшифровать аналогичные спиральные узоры в шишках, ананасах и цветной капусте, которые также отражают последовательность Фибоначчи.

Романская цветная капуста (Источник: science.howstuffworks.com)

Голова подсолнуха (Источник: hynesva.com)

Ниже приведены изображения поперечных сечений морской раковины Наутилуса.Они показывают спиралевидный изгиб панциря и внутренние камеры, которые животное, использующее его, добавляет по мере своего роста. Камеры обеспечивают плавучесть на воде.

Поперечное сечение показывает золотую спираль (Источник: asal-sakti.blogspot.com)

Nautilus Shell (Источник: amazingdata.com)

Рыба-ангел Каждая ключевая особенность тела рыбы-ангела выпадает на золотые сечения ее ширины и длины. Нос, хвостовая часть и центры плавников рыбы-ангела попадают в первые (синие) золотые сечения.Второе золотое сечение (желтое) определяет углубления на спинной и хвостовой находках, а также на верхней части тела. Зеленая часть определяет отметку вокруг глаза, а пурпурная часть определяет глаз. (Источник: goldennumber.net)

Некоторые растения выражают последовательность Фибоначчи в своих точках роста , местах, где ветви деревьев образуются или разделяются. Один ствол растет, пока не образуется ветка, в результате чего образуются две точки роста. Затем основной ствол дает еще одну ветвь, в результате чего образуются три точки роста.Затем ствол и первая ветвь производят еще две точки роста, в результате чего общее количество достигает пяти. Эта модель продолжается, следуя числам Фибоначчи.
(Источник: journalofcosmology.com)

• 4б. В человеческом теле:

«Витрувианский человек» — всемирно известный рисунок, созданный Леонардо да Винчи около 1487 года. Тело окружено квадратом, а руки и ноги касаются круга с пупком в центре. Фигура разделена пополам в паху и золотым сечением в пупке.Рисунок основан на соотношениях идеальных человеческих пропорций с геометрией, описанных древнеримским архитектором Витрувием в Книге III его трактата De Architectura .
(Источник: sistertongue.wordpress.com)

На иллюстрации, приведенной ниже, мы можем увидеть несколько случаев золотого сечения в человеческом теле.

1. Подошва к пупку: Подошва к макушке.
2. Подошва до колена: подошва до пупка.
3. От пупка к плечу: от пупка к макушке.
4. Колено до икроножной мышцы: Колено до подошвы.
5. От пупка до середины бедра: от пупка до колена.
6. От пупка до середины груди: от пупка до основания горла.
7. От основания горла до виска: от основания горла до макушки.
8. От икроножной мышцы до голеностопного сустава: от икроножной мышцы до подошвы.
9. От середины бедра до начала коленной чашечки: от середины бедра до конца коленной чашечки.
10. От пупка до промежности: от пупка до середины бедра.
11. От пупка до основания грудины: от пупка до грудины или середины груди.
12. От основания горла до мочки уха: от основания горла до верхней части уха.
13. От надбровной кости до линии роста волос: от надбровной кости до темени.
14. От носа к подбородку: от носа к основанию горла

(Источник: beautifulproportion.com)

Для идеальной улыбки два передних зуба образуют золотой прямоугольник. Также существует золотое сечение между высотой и шириной двух центральных зубов. А отношение ширины двух центральных зубов к ширине соседних — фи. Отношение ширины улыбки к третьему зубу от центра тоже фи.
(Источник: библиотека.thinkquest.org)

В легких человека дыхательное горло делится на два основных бронха: один длинный (левый) и короткий (правый). Это асимметричное деление продолжается и на последующие подразделения бронхов. Было установлено, что во всех этих отделах отношение короткого бронха к длинному всегда составляло 1 / 1,618.
(Источник: library.thinkquest.org)

Даже молекула ДНК, программа для всей жизни, основана на золотом сечении.Он измеряет 34 ангстрем в длину и 21 ангстрем в ширину для каждого полного цикла двойной спирали. 34 и 21, конечно же, являются числами в ряду Фибоначчи, и их отношение, 1,61

, близко приближается к Фи, 1,6180339.
(Источник: sites.google.com/site/chsscience/)

Мона-Лиза, Леонардо да Винчи
(Источник: sinearch.com)

Святое Семейство, Микаеланджело
Основные фигуры выровнены с пентаграммой или золотой звездой.
(Источник: fabulousfibonacci.com)

Автопортрет Рембрандта
Треугольник пересекает основание в золотом сечении.
(Источник: jwilson.coe.uga.edu)

Таинство Тайной вечери
— Сальвадор Дали
Картина написана внутри золотого прямоугольника.
(Источник: goldennumber.net)

Парфенон
(Источник: britton.disted.camosun.bc.ca)

Великая пирамида в Гизе
(Источник: jwilson.coe.uga.edu)

Статуя Афины
( Источник: library.thinkquest.org )

• 4д. In Music:
В дополнение к существованию в природе, искусстве и архитектуре, была выдвинута гипотеза, что великие классические композиторы, такие как Моцарт, знали о золотом сечении и использовали его для составления некоторых из своих знаменитых сонат.Золотое сечение проявляется в соотношении интервалов или расстояния между нотами. Музыкальные весы основаны на числах Фибоначчи. В диапазоне любой ноты до октавы 13 нот. Шкала состоит из 8 нот, из которых 5-я и 3-я ноты составляют основу всех аккордов и основаны на целом тоне, который находится на 2 шага от основного тона, то есть 1-й ноты шкалы.

Euclid — построение золотого сечения — ETH Library

«Элементы» (издание 1482 г.), написанные в тринадцати книгах, т.е.е. Тринадцать глав — это самая известная и наиболее значимая с научной точки зрения работа греческого математика Евклида. После Библии это самая печатаемая и изученная книга в истории западного мира.

Даже сегодня большая часть математического и геометрического начального образования основана на евклидовой традиции. «Элементы» Евклида представляют геометрию как логически самодостаточную систему, построенную на горстке определений, постулатов и аксиом. Помимо систематического представления основных геометрических терминов, он содержит все, что было известно в то время о теории чисел.Здесь также впервые были сделаны важные открытия относительно простых чисел.

• Книги с 1 по 4 имеют дело с геометрией плоскости и ведут от элементарных свойств точек, прямых и углов, среди прочего, к теореме Пифагора. В Книге 2, Предложении 11, проиллюстрированном выше, объясняется построение «прямой линии, разрезанной в крайнем и среднем отношении», то есть в пропорции, ныне известной как золотое сечение.
• Книги 5 и 6 охватывают пропорции и аналогичные фигуры. Начало Книги 6 также содержит определение «прямой разрез в крайнем и среднем соотношении».
• Книги с 7 по 9 посвящены арифметике, то есть свойствам натуральных чисел. Здесь вы можете найти «алгоритм Евклида», используемый для определения наибольшего общего делителя двух заданных целых чисел.
• Книга 10 касается несоизмеримых величин, то есть иррациональных чисел.
• Наконец, книги с 11 по 13 охватывают пространственную геометрию и пять правильных (платонических) твердых фигур.

Как показывает проблема из «Liber abaci», Фибоначчи был знаком — в традиции Евклида — с концепцией пропорции в соответствии с тем, что впервые было названо золотым сечением в девятнадцатом веке.Но он не установил никакой связи между этим соотношением и последовательностью чисел, которую он нашел в задаче о кроликах.

(PDF) Простое построение золотого сечения

World Applied Sciences Journal 7 (7): 833-833, 2009

ISSN 1818-4952

© IDOSI Publications, 2009

Автор для корреспонденции: д-р Абдулла Каплан, Университет Ататюрка KK Образовательный факультет,

Департамент математического образования, Эрзурум, Турция

833

Простое построение золотого сечения

Абдулла Каплан, Нилгюн Тортумлу и Сейфуллах Хизарчи

Университет Ататюрка К.K. Педагогический факультет, Департамент математического образования, Эрзурум, Турция

Аннотация: У геометрии есть два великих сокровища. Одна из них — это теорема Пифагора, а другая — деление

отрезка прямой на равное и среднее соотношение. Первую мы можем назвать «порцией золота», а другую — «драгоценным камнем

». Идея Кеплера привела нас к тому, как найти золотое сечение в трапеции. И мы

открыли это золотое сечение за четыре шага. Мы строим золотое сечение, используя биссектрису трапеции

.

Ключевые слова: Золотое сечение

• трапеция

ВВЕДЕНИЕ

Пусть | AD | = a, | BC | = b, a

ABCD. Найдем золотую точку, которая делит

| AD | с золотым сечением за несколько шагов. [1-3]

• Нарисуем BC⊥ EC и | CE | = | AD | = a (Рис. 1)

• Если средняя точка | EB | is F,

ab

EF BF

2

+

= =

• Возьмем | BF | = | FG | в состоянии | BE | ⊥ | FG |

• Нарисуем окружность с радиусом B (BG) и

B (BG) ∩ [BC] = H

• [KL] // [BC] и

ab

BH KL BG

2

+

= = =

.

Рис. 1: Золотое сечение в трапеции

• Нарисуем [AN] // [DC]. Это | BN | = ba и

22

ab

PL a

2

+

= —

• Мы можем найти уравнение

22

ab

a

AL PL

2 AB BN ba

+

—

= =

—

Уравнение седьмое должно быть равно

51

2

—

, чтобы получилось

, а точка L — золотая точка.